Gehirntheorie der Wirbeltiere
ISBN
978-3-00-064888-5
Monografie von Dr. rer. nat. Andreas Heinrich Malczan
5.2 Die Theorie der ebenen Divergenzgitter
Wir analysieren nun die Funktionsweise von ebenen Divergenzgittern am Beispiel eines solchen mit vier Inputneuronen. Divergenzgitter mit zwei Inputneuronen sind bereits analysiert worden. Ausgangspunkt war die Kabelgleichung für marklose Axone, die an dieser Stelle nochmals wiedergegeben wird.
Die Kabelgleichung für marklose Axone beschreibt die Abnahme der Erregung entlang eines Axons, wobei E0 die Ausgangserregung am Axonanfang darstellt und E dem Erregungswert entspricht, der im Abstand x vom Axonanfang gemessen wird:
![]() .
.
Die Größe λ wird als Längskonstante des Neurons bezeichnet.
Die Erregungsfunktion kann grafisch in einem Diagramm dargestellt werden, hier ist die Erregungsabnahme bei zunehmendem Abstand gut zu erkennen.
Aus der Kabelgleichung für marklose Fasern kann direkt auf die Feuerrate f geschlossen werden, die ein Neuron hat, welches von einem Inputneuron mit der Feuerrate f0 den Abstand x hat und mit diesem über ein markloses Axon verbunden ist. Hier tritt anstelle der Erregung E die Feuerrate f auf.
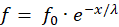
Die grafische Darstellung der Feuerratenfunktion in Abhängigkeit vom Abstand x zeigt die nachfolgende Abbildung.
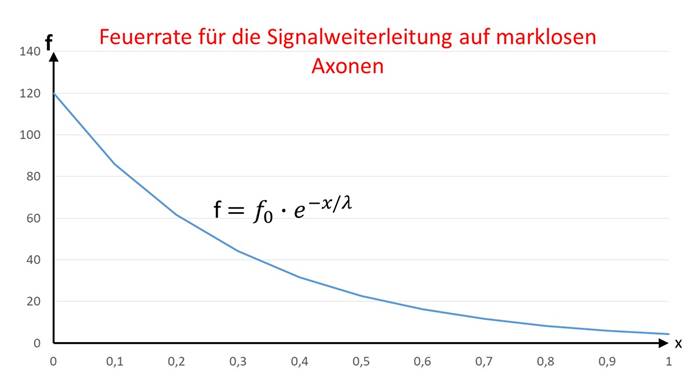
Abbildung 45 - Feuerrate für die Signalweiterleitung auf marklosen Fasern
In einem linearen Divergenzgitter überlagerten sich die Erregungen von zwei Neuronen. In einem ebenen Divergenzgitter erfolgt die Ausbreitung der Erregung in der Fläche, in der sowohl die Inputneuronen als auch die Outputneuronen verteilt sind.
Wir vergleichen beide Divergenzgitter in nachfolgender Abbildung, die bereits verwendet wurde.
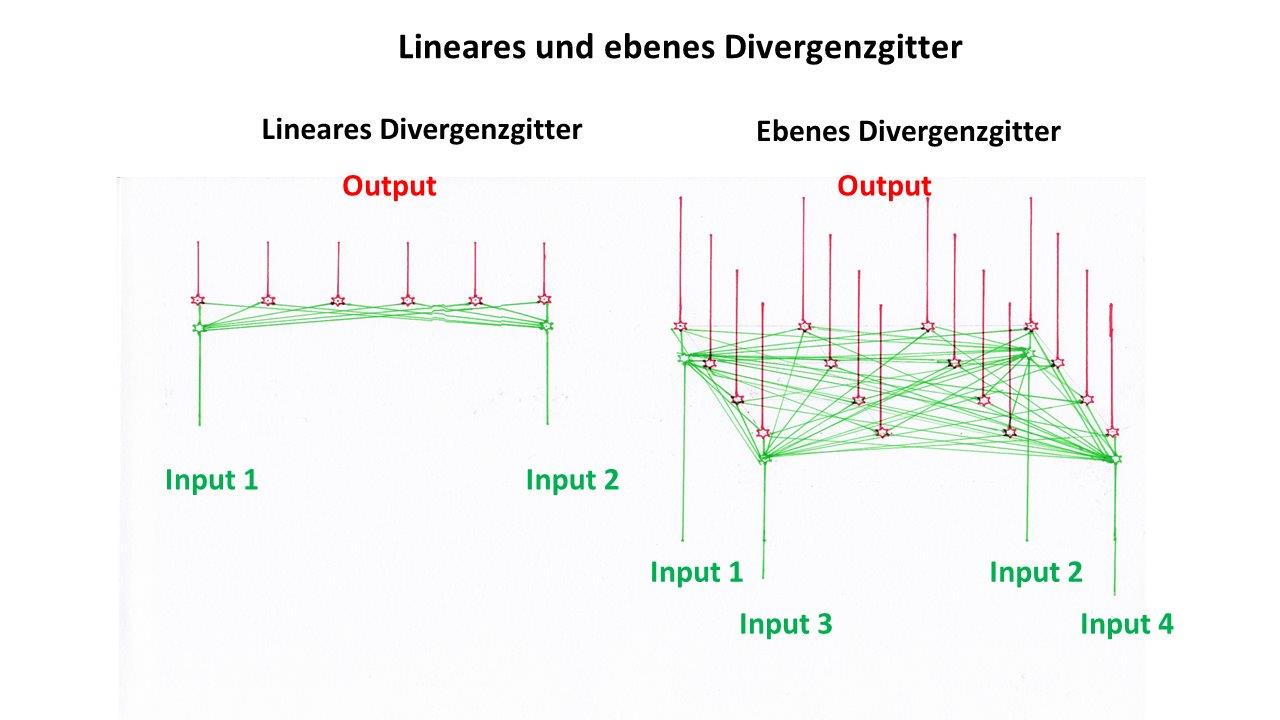
Abbildung 46 - Lineares und ebenes Divergenzgitter im Vergleich
Das ebene Divergenzgitter möge vier Inputneuronen besitzen. Wir ordnen die vier Inputneuronen in einem Koordinatensystem so an, dass sie im Abstand 1 vom Nullpunkt jeweils auf den Koordinatenachsen liegen, wie nachfolgende Abbildung zeigt.
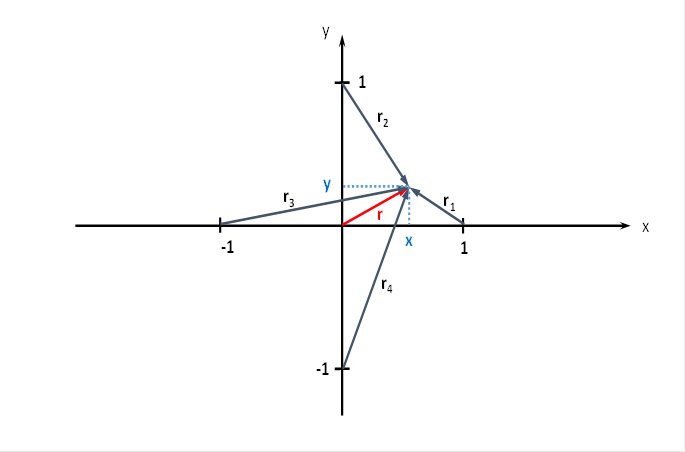
Abbildung 47 - Ebenes Divergenzgitter mit vier Inputneuronen
Im Punkt P mit den Koordinaten P = (x ; y), zu dem der Radiusvektor r gehört, möge sich - stellvertretend für die vielen hundert Outputneuronen - ein Outputneuron befinden, dessen Erregung wir berechnen möchten.
Uns interessiert die Erregung derjenigen Neuronen, die sich im Quadrat mit der Seitenlänge 2 befinden, dessen Mittelpunkt im Koordinatenursprung liegt. Jedes der dort befindlichen Outputneuronen ist mit den vier Inputneuronen synaptisch verknüpft, so wie es die obige Abbildung zum ebenen Divergenzgitter zeigt. Insbesondere interessieren uns die Extremwerte der Erregungen in diesem Quadrat, also Minima und Maxima. Dazu müssen wir einige mathematische Überlegungen anstellen.
Für die beteiligten Radiusvektoren r1 bis r4 erhält man über den Satz des Pythagoras nachfolgende Gleichungen:
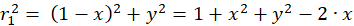 (3.1)
(3.1)
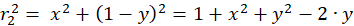 (3.2)
(3.2)
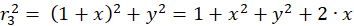 (3.3)
(3.3)
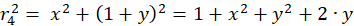 (3.4)
(3.4)
Während im linearen Divergenzgitter die exponentielle Dämpfung mit der Entfernung zunahm, unterstellen wir im ebenen Divergenzgitter eine quadratische exponentielle Dämpfung , weil sich die Erregung der Inputneuronen nicht entlang einer Geraden, sondern innerhalb einer Fläche ausbreiten muss.
Befinden sich
die vier Inputneuronen in den Punkten
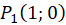 ,
,
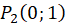 ,
,
 und
und
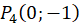 und
erhalten die Erregungen mit den Feuerraten f1, f2, f3
und f4, so kann unter unseren Voraussetzungen die Feuerrate f des
Outputneurons
im Punkt
und
erhalten die Erregungen mit den Feuerraten f1, f2, f3
und f4, so kann unter unseren Voraussetzungen die Feuerrate f des
Outputneurons
im Punkt
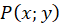 als
Summe berechnet werden:
als
Summe berechnet werden:
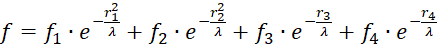 .
(3.5)
.
(3.5)
Setzt man für die vier Radiusvektoren r1 bis r4 die Beziehungen (3.1) bis (3.4) ein und fasst die gemeinsamen Faktoren zusammen, so ergibt sich folgendes:
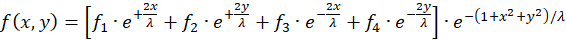 (3.6)
(3.6)
Hier sind x und y die Koordinaten des Outputneurons im Punkt P(x,y) im kartesischen Koordinatensystem.
Wir gehen davon aus, dass die Erregungen f1 bis f4 von vier Rezeptoren geliefert werden. Je zwei von ihnen müssen beim Divergenzgitter zueinander komplementär sein, also durch Signalinversion auseinander hervorgehen. Es könnten die Signale zweier gegeneinander arbeitender Muskeln sein. Wir wählen f1 und f3 als erstes Paar zueinander komplementärer Signale, die von den Rezeptoren R1 und R3 geliefert werden.
Für diese zwei Rezeptorsignale wählen wir den exponentiellen Ansatz gemäß
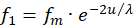 (3.7)
(3.7)
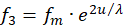 (3.8)
(3.8)
Hierbei könnte die Urgröße u beispielsweise dem Gelenkwinkel entsprechen.
Neurologen werden (berechtigterweise) einwenden, dass eine exponentielle Kennlinie nicht allgemein akzeptiert wird. Von vielen wird angenommen, der Zusammenhang zwischen einer Urgröße und der Feuerrate der wahrnehmenden Rezeptoren wäre logarithmisch. Wir beziehen uns in dieser Monografie jedoch (zunächst) auf den motorischen Bereich. Es scheint unrealistisch, anzunehmen, die Muskelzugkraft müsse sich vervierfachen, damit sich die Feuerrate z. B. der Muskelspindeln verdopple. Denn das bedeutet auch, dass die Muskelzugkraft um den Faktor 25 zunehmen muss, damit die Feuerrate sich verfünffacht. Oder die Muskelzugkraft müsse um den Faktor 100 vergrößert werden, damit die Feuerrate um den Faktor 10 steige. Solche Zugkräfte an Muskeln sind unrealistisch und würden zu ihrer Zerstörung führen.
Wir wählen den exponentiellen Ansatz. Dies ist viel realistischer.
In anderen Gebieten, beispielsweise im visuellen Bereich, kommen Regelmechanismen zum Einsatz, die eine logarithmische Kennlinie bewirken. Hier kann die Lichtstärke durch die Pupillenverengung geregelt werden, außerdem gibt es unter den Sehrezeptoren eine geregelte Hemmungswirkung etwa durch die amakrinen Zellen, die mit der Helligkeit zunimmt.
Wir wählen für die Urgröße u den Gelenkwinkel, dessen Messwert vom zuständigen Rezeptor (z. B. dem Sehnenorgan) in eine Feuerrate mit exponentieller Empfindlichkeitskurve transformiert wird. Die Größe fm stellt die mittlere Feuerrate dar. Sie wird vom Rezeptor geliefert, wenn die Urgröße u genau in der Mitte des zugehörigen Messintervalls <u1; u2> liegt.
Und da jedes Gelenk zwei gegeneinander arbeitende Muskeln besitzt, ergeben sich die beiden Feuerraten f1 und f3. Sie sind invers zueinander.
Die Feuerrate f1 ist streng monoton fallend, also vom Off-Typ. Die Feuerrate f3 dagegen ist streng monoton wachsend und daher vom On-Typ. Für eine neuronale Signalauswertung werden immer beide Feuerraten und somit auch beide Rezeptoren benötigt.
Analog möge es für die zwei übrigen Feuerraten f2 und f4 ebenfalls zwei Rezeptoren R2 und R4 geben, die den Wert einer anderen Urgröße v ebenso in zwei zueinander komplementäre Feuerraten übertragen, die mittlere Feuerrate sei die gleiche.
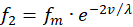 (3.9)
(3.9)
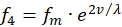 (3.10)
(3.10)
Auch hier ist wieder eine Feuerrate streng monoton fallend und die andere steigend.
Im ebenen Divergenzgitter gehen die Urgrößen u und v mit dem Faktor 2 in die Exponenten der Feuerrate ein, da wir auch eine quadratische Berücksichtigung des Abstandes in der Erregungsfunktion angenommen haben. Daher müssen auch die Rezeptoren einen stärkeren Input liefern, damit bei den Empfängerneuronen im ebenen Divergenzgitter überhaupt eine brauchbare Erregung ankommt, denn diese muss sich ja in der Fläche ausbreiten. Auch die Neuronen, die diese Erregung im ebenen Divergenzgitter in der Fläche weiterleiten, sind stärker und größer.
Die Größen u und v stellen in diesen Feuerraten die Stärke von gemessenen Urgrößen dar, die von den vier Rezeptoren geliefert wird. Warum aber ordnen wir f1 zu f3 und f2 zu f4 und nicht etwa f1 zu f2 und f3 zu f4? Weil wir die Anordnung so wählen, wie sie etwa bei einem Gelenk mit zwei Freiheitsgraden zu finden ist. Während f1 dem Beuger und f3 dem Strecker für den einen Freiheitsgrad zugeordnet ist, sind f2 und f4 für den zweiten Freiheitsgrad zuständig. Daher wäre die Anordnung der zugehörigen Muskeln und Sehnen am Gelenk genauso, wie wir es bei den zugeordneten Feuerraten gewählt haben.
Setzen wir die obigen Feuerraten (3.7) bis (3.10) in die Gleichung (3.6) ein, so ergibt sich für die Erregung eines Outputneurons im Punkt P(x,y) die Funktionsgleichung
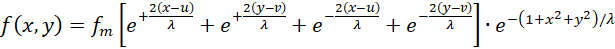 (3.11)
(3.11)
Die Verwendung der Hyperbelfunktion
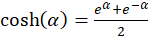 (3.12)
(3.12)
liefert die Vereinfachung
 (3.13)
(3.13)
Nun können wir analysieren, welche Wirkungen die Veränderungen der von den Rezeptoren R1 bis R4 gemessenen Größen u und v auf die Erregung eines Outputneurons haben.
Im linearen Divergenzgitter hatte die Erregungsfunktion ein Minimum, welches letztlich die Stärke der gemessenen Urgröße verschlüsselte. Wie verhält es sich mit der Erregungsfunktion im ebenen Divergenzgitter? Gibt es irgendeinen wesentlichen Unterschied?
Diese Frage muss bejaht werden. Im ebenen Divergenzgitter wird die Stärke der Urgrößen nicht über ein Erregungsminimum verschlüsselt, sondern über ein Erregungsmaximum. Die Erregungsfunktion (3.11) bzw. (3.13) besitzt ein Erregungsmaximum in der Nähe des Punktes P(u,v).
Theorem der Maximumcodierung der Urgrößen im ebenen Divergenzgitter mit vier Inputneuronen
Es sei u eine Urgröße, deren Wert mittels zweier komplementärer Rezeptoren R1 und R3 in zwei zueinander komplementäre Feuerraten f1 und f3 transformiert wird gemäß
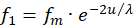 und
und
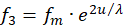 .
.
Es sei v eine
weitere, davon unabhängige
Urgröße, deren Wert mittels zweier
komplementärer Rezeptoren R2 und R4
in die zueinander komplementären Feuerraten f2
und f4
transformiert wird gemäß
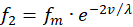 und
und
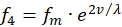
Ein ebenes Divergenzgitter empfange - bezogen auf ein kartesisches Koordinatensystem - die vier Feuerraten wohlgeordnet derart, dass f1 im Punkt P(1,0), f2 im Punkt P(0,1), f3 im Punkt P(-1,0) und letztlich f4 im Punkt P(0,-1) als Input wirksam wird.
Dann hat die Erregungsfunktion f(x,y) die Form

und besitzt für beliebige u und v aus dem Intervall <-1; +1> ein Erregungsmaximum im Punkt P(xo; yo), und für die Koordinaten xo und yo des Maximumpunktes gelten die Beziehungen
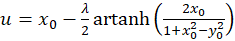 (3.14)
(3.14)
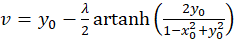 (3.15)
(3.15)
Zu jedem Punkt P(xo, yo) kann über die Gleichungen (3.14) und (3.15) berechnet werden, welchen Wert die Urgrößen u und v haben müssen, damit die neuronale Erregung in diesem Punkt ihr Maximum annimmt.
Eine kleine Einschränkung für u und v ergibt sich daraus, dass die Funktion artanh(x) nicht für alle x definiert ist. Aus neurologischer Sicht interessieren uns auch nur die Maxima innerhalb des Quadrates mit der Seitenlänge 2, dessen Zentrum vom Koordinatenursprung gebildet wird und in dem sich die Outputneuronen befinden.
Zur Herleitung der Bedingungen (3.14) und (3.15) müssen wir die Funktion (3.13) in eine bequemer zu handhabende Form bringen.
 (3.16)
(3.16)
Hierbei
gilt s = x + y und d = x - y, also
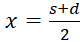 und
und
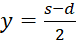 .
.
Daraus folgt
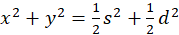 (3.17)
(3.17)
Damit wird (3.16) zu
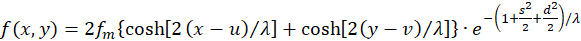 (3.18)
(3.18)
Nun formen wir den Ausdruck mit den Hyperbelfunktionen um.
Wegen
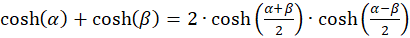 (3.19)
(3.19)
gilt
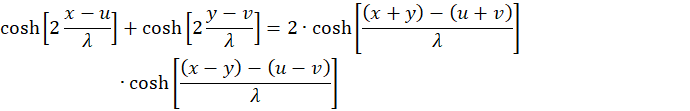
Wir setzen u + v = w sowie u - v = z und erhalten wegen x + y = s und x - y = d die Gleichung
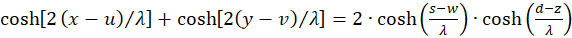 (3.20)
(3.20)
So erhält (3.13) eine neue Darstellung:
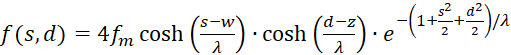 (3.21)
(3.21)
Diese Darstellung ist leichter handhabbar beim Differenzieren, da die Variablen s und d in getrennten Faktoren auftauchen.
Für die Ermittlung von Extremwerten berechnen wir die zunächst die erste Ableitung sowohl nach s als auch nach d.
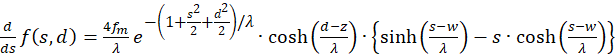 (3.21)
(3.21)
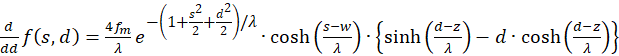 (3.22)
(3.22)
Die Ableitungen nach s und nach d müssen gleich null sein, damit überhaupt ein Extremwert vorhanden sein kann (notwendige Bedingungen). Da die mittlere Feuerrate fm sowie λ größer als null sind, der Exponentialausdruck generell größer als null ist und letztlich die Funktion cosh(x) größer als 1 ist, muss jeweils der letzte Faktor in dem Klammerausdruck gleich null sein. So erhalten wir zwei Bedingungsgleichungen für die Werte so und do, in denen ein Extremwert vorliegen könnte.
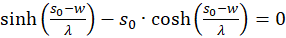 und
und
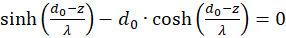 .
(3.23)
.
(3.23)
Umformen ergibt:
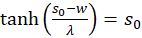 und
und
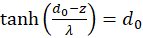 (3.24)
(3.24)
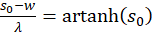 und
und
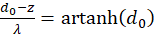 (3.25)
(3.25)
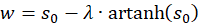 und
und
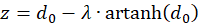 (3.26)
(3.26)
Wegen u + v = w sowie u - v = z und x + y = s und x - y = d ergibt sich
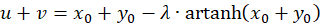 (3.27)
(3.27)
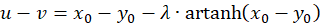 (3.28)
(3.28)
Addition beider Gleichungen liefert
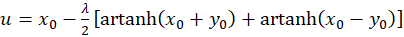 (3.29)
(3.29)
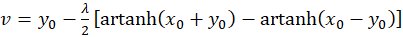 (3.30)
(3.30)
Wir drücken x und y durch Polarkoordinaten aus und berücksichtigen die Abbildung 49. Dann gilt:
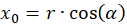
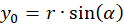
Das Einsetzen in obige Gleichung und die Anwendung von Additionstheoremen für Winkelfunktionen liefert:
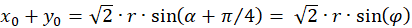 (3.31)
(3.31)
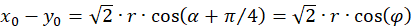 (3.32)
(3.32)
mit
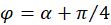 .
(3.33)
.
(3.33)
Dann gilt:
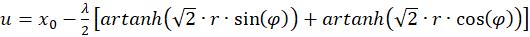 (3.34)
(3.34)
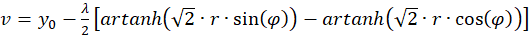 (3.35)
(3.35)
Da die Funktion f(x) = artanh(x) nur für x-Werte mit -1 ≤ x ≤ +1 definiert ist, also gibt es für die Größen r und α die zwei Bedingungen

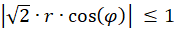 .
.
Dies bedeutet:
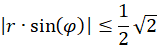
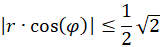
Für den Radiusvektor r bedeutet dies folgende Bedingung für das Vorliegen eines Extremwertes:
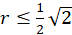 (3.36)
(3.36)
Die Anwendung des folgenden Additionstheorems auf (3.29) und 3.30 bietet sich an:
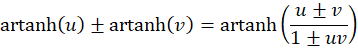
und liefert die Extremwertbedingung
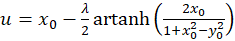 (3.37)
(3.37)
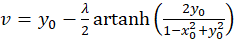 (3.38)
(3.38)
Verwendet man dagegen die Darstellung in Polarkoordinaten gemäß (3.31) und (3.32), so ergibt sich als Extremwertbedingung:
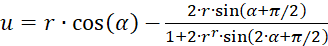 (3.39)
(3.39)
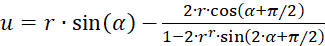 (3.40)
(3.40)
Die Gleichungen (3.36) und (3.37) bzw. (3.38) und (3.32) sowie (3.39) und (3.40) müssen erfüllt sein, damit die Erregungsfunktion (3.13) einen Extremwert im Punkt(xo, yo) besitzt. Sie erlauben zwar nicht die Bestimmung von x und y, jedoch können zu jedem beliebigen Wert von x und y aus dem Definitionsbereich die erforderlichen Werte für die Urgrößen u und v ermittelt werden, so dass dort ein Extremwert vorliegen kann.
Dazu müssen jedoch auch die hinreichenden Bedingungen erfüllt sein, die für das Vorhandensein von Extremwerten gelten.
Wir erinnern uns:
Ist an der Stelle so und do fs(so, do) = 0 und fd(so, do) = 0 und besteht die Ungleichung
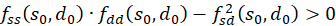 ,
(3.41)
,
(3.41)
so liegt an dieser Stelle ein Minimum vor, wenn
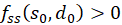 ist
und ein Maximum, wenn
ist
und ein Maximum, wenn
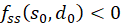 ist.
ist.
Wir gehen in mehreren Schritten vor.
(1) Zunächst beweisen wir, dass
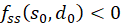 ist.
ist.
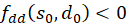 ist.
ist.
Damit ist das Produkt
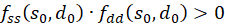 .
.
Weiter zeigen wir, dass
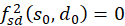 ist.
Damit wäre die Ungleichung 3.41 bewiesen. Und da die zweite Ableitung nach s
negativ ist, würde bewiesen sein, dass ein Maximum vorliegt.
ist.
Damit wäre die Ungleichung 3.41 bewiesen. Und da die zweite Ableitung nach s
negativ ist, würde bewiesen sein, dass ein Maximum vorliegt.
Wir weisen zunächst (1) nach.
Dazu berechnen wir die zweite Ableitung, die wir der besseren Übersicht wegen gleich als Produkt zweier Faktoren schreiben:
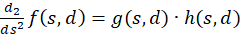 (3.42)
(3.42)
mit
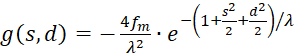
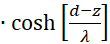 (3.43)
(3.43)
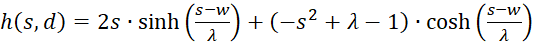 (3.44)
(3.44)
Der Faktor g(s,d) ist generell negativ für alle Werte von s, d und w.
Wir prüfen daher nur noch, ob der Faktor h(s,d) im Punkt P(so, do) positiv ist, weil dann das Produkt beider negativ und eine von zwei hinreichenden Bedingungen für die Existenz eines Maximums erfüllt wäre. Dazu erinnern wir uns an die Gleichung (3.23):
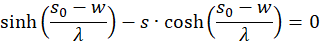
Umstellen liefert
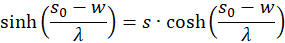
Dies setzen wir in Gleichung (3.44) ein und beachten x = xo und y = yo:
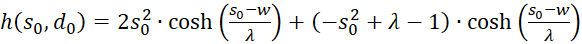 (3.45)
(3.45)
Wir fassen zusammen:
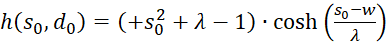 (3.46)
(3.46)
Unter Beachtung von λ > 1 gilt für beliebige Werte die Ungleichung
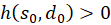
und damit auch
Damit ist die zweite Ableitung nach s kleiner als Null, so dass (1) bewiesen wäre.
Nun weisen wir (2) nach.
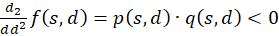 (3.48)
(3.48)
mit
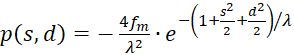
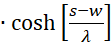 (3.49)
(3.49)
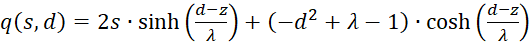 (3.50)
(3.50)
Der erste Faktor ist wieder negativ. Der zweite ist positiv, weil wir substituieren können. Nach (3.23) gilt
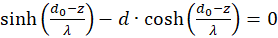
Wir formen um:
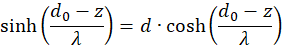
Einsetzen in (3.50) ergibt für s = so und d = do
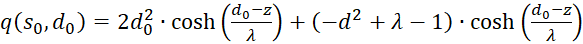 (3.51)
(3.51)
Zusammenfassen liefert
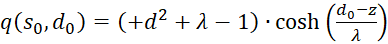 (3.52)
(3.52)
Wegen λ > 1 gilt nun generell
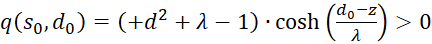 (3.53)
(3.53)
Da p(s,d) kleiner als Null war und q(s,d) größer als Null, ist das Produkt beider negativ.
Damit gilt für die zweite Ableitung nach d ebenfalls die Gleichung
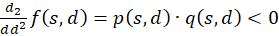 (3.54)
(3.54)
Die Gleichung
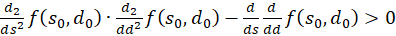 (3.55)
(3.55)
wäre immer erfüllt, wenn folgendes nachweisbar wäre:
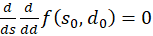 (3.56)
(3.56)
Wir berechnen diese gemischte Ableitung und stellen die als Produkt von drei Faktoren dar:
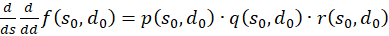 (3.57)
(3.57)
Es gilt
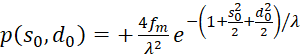 (3.58)
(3.58)
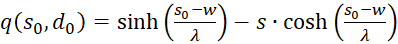 (3.59)
(3.59)
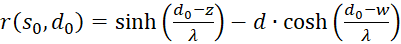 (3.60)
(3.60)
Die Faktoren
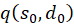 und
und
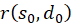
sind jedoch gleich null, wie bereits bei (3.23) gezeigt wurde. Damit ist auch die gemischte Ableitung gleich null. Somit besitzt unsere Erregungsfunktion ein Maximum bei den hergeleiteten Koordinaten. Damit ist das Theorem der Maximumcodierung im ebenen Divergenzgitter mit vier Inputneuronen bewiesen.
Für die nachfolgenden Betrachtungen wählen wir wieder die Darstellung der Erregungsfunktion in den Variablen x und y.
Wir können uns nun eine Vorstellung davon erarbeiten, wie die zweidimensionale Erregungsfunktion f(x,y) aussieht und an dass sie an der entsprechenden Stelle, die nahe am Punkt P(u,v) liegt, tatsächlich ein Maximum hat.
|
Abbildung 48-Prinzipdarstellung Nr. 1 Erregungsfunktion
|
Abbildung 49- Prinzipdarstellung Nr. 2 Erregungsfunktion |
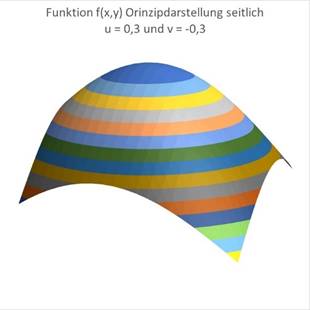
Für u = 0,3 und v = -0,3 wandert das Maximum nach links und nach hinten:
|
Abbildung 50- Prinzipdarstellung Nr. 3 Erregungsfunktion |
Abbildung 51- Prinzipdarstellung Nr. 4 Erregungsfunktion |
Für u = -0,3 und v = +0,3 wandert das Maximum nach rechts und nach vorn:
|
Abbildung 52- Prinzipdarstellung Nr. 5 Erregungsfunktion |
Abbildung 53-Prinzipdarstellung Nr. 6 Erregungsfunktion |
In ebenen Divergenzgittern tritt häufig eine laterale Hemmung auf. Stark erregte Neuronen hemmen schwächer erregte über zwischengeschaltete hemmende Interneuronen. Dadurch bleibt die Erregung in der Umgebung des Ortes mit der Maximalerregung erhalten, während sie im übrigen Gebiet des quadratischen Divergenzgitters völlig gehemmt wird. Dadurch entsteht der Eindruck einer stark erregten Neuronenpopulation, die bei Veränderung der Urgrößen u und v im ebenen Divergenzgitter herumwandert. Bei periodischen Bewegungen entstehen die erwähnten Lissajous-Figuren.
Theorem der Extremwertselektion in ebenen Divergenzgittern
Eine starke laterale Hemmung in ebenen Divergenzgittern mit Maximumcodierung bewirkt, dass nur um die Stelle des Maximums eine aktive Neuronenpopulation beobachtet wird.
Die Signaldivergenz trat als erstes im Nucleus olivaris auf. Dort wurde der Input von zueinander komplementären Signalen in minimumcodierte Signale transformiert, die anschließend im Kleinhirnkern invertiert wurden, so dass sie wieder maximumcodiert waren.
Bei einer Signaldivergenz im ebenen Divergenzgitter mit Maximumcodierung entstehen direkt maximumcodierte Signale. Eine Signalinversion, wie sie im Kleinhirnkern erfolgte, würde wieder unbrauchbare minimumcodierte Signale liefern. Daher war der Nucleus olivaris für solche ebenen Divergenzgitter unbrauchbar.
Ebene Divergenzgitter mussten also an anderer Stelle im Gehirn entstehen, auch wenn sie primär überhaupt nicht für eine Maximumcodierung von Signalen entwickelt wurden. Der Hauptvorteil der ebenen Divergenzgitter lag zunächst in der Erhöhung der Ausfallsicherheit. Signale wurden redundant auf Gruppen von Neuronen übertragen, die jeweils ein ebenes Divergenzgitter bildeten. Fielen einzelne Neuronen aus, erhielten die Zielstrukturen dennoch ihren Input.
Dass sich auf Grund der exponentiellen Signaldämpfung eine Maximumcodierung der Stärke der Urgrößen ergab, war - wie alles in der Evolution - nicht geplant, sondern die zufällige Folge des Wirkens von Naturgesetzen bei der Ausbreitung von Aktionspotentialen auf marklosen Axonen.
Hier muss darauf hingewiesen werden, dass die hergeleitete Maximumcodierung nur dadurch eintritt, dass in einem Gelenk mit mehreren Freiheitsgraden die Muskelspannungsrezeptoren der Muskeln für die verschiedenen Bewegungsebenen miteinander gekoppelt sind. Bei nicht gekoppelten Größen können ebene Divergenzgitter durchaus auch minimumcodierte Signale liefern. Verallgemeinert treten hier extremwertcodierte Signale auf. Im visuellen Bereich gibt es für das Farbsehen eine Minimumcodierung, für das Formensehen jedoch eine Maximumcodierung. Dies wird in weiteren Kapiteln aufgezeigt.
Natürlich entsteht die Frage, ob ebene Divergenzgitter im Wirbeltiergehirn tatsächlich vorhanden sind?
Suchen kann man solche Divergenzgitter nur in Neuronenflächen, die zur grauen Substanz gehören, denn die Axone, die die Erregung divergent weiterleiten, müssen marklos sein. Sie dürfen also keine Myelinscheiden besitzen, die für die weiße Substanz typisch sind. In Frage kommen also alle Kerne der grauen Substanz und die Cortexrinde. Weiterhin muss die Anzahl der Outputneuronen die der Inputneuronen deutlich übertreffen. Damit scheiden viele Neuronenkerne aus. Letztlich muss in diesen Neuronenflächen eine Maximumcodierung nachgewiesen werden. Damit scheidet der Nucleus olivaris völlig aus, und es bleibt fast nur noch der Cortex übrig. Vergessen werden sollten jedoch nicht die Kerne der grauen Substanz im limbischen System, insbesondere der Amygdala. Und bei Vögeln und Reptilien wären da noch der DVR sowie bei Vögeln das Hyperpallium.
Ein weiteres Problem ist die Existenz von Konvergenzgittern, die genau invers zu den Divergenzgittern arbeiten und prinzipiell den gleichen Aufbau haben, nur dass Input und Output vertauscht sind. Daher haben Konvergenzgitter deutlich weniger Outputneuronen als Inputneuronen - ein wichtiges Differenzierungsmerkmal.
Bei Säugern findet man Konvergenzgitter im Cortex.
Theorem der Existenz von ebenen Divergenzgittern im Cortex
Diejenigen primären Cortexgebiete, die ihren Rezeptorinput über Thalamuskerne und nicht über das Cerebellum empfangen, bestehen aus ebenen Divergenzgittern. Die Topologie der sensorischen Körpermodelle bleibt in diesen Cortexgebieten trotz der Signaldivergenz erhalten.
Damit ergibt sich die nächste Frage: Welche Belege gibt es für die Arbeit von ebenen Divergenzgittern in den primären Cortexgebieten? Dieser Frage widmet sich das folgende Kapitel.
Zuvor müssen wir uns mit der Funktionsweise von ebenen Konvergenzgittern informieren.
-
← 5.1 Rekapitulation der bisherigen
Entwicklung
und Vorschau auf die Weiterentwicklung -
5.3 Urgrößendiagramm, Bilddiagramm,
Radiusvektor
und Phasenwinkel in ebenen Divergenzgittern →
Monografie von Dr. rer. nat. Andreas Heinrich Malczan