Gehirntheorie der Wirbeltiere
ISBN
978-3-00-064888-5
Monografie von Dr. rer. nat. Andreas Heinrich Malczan
5.6 Die Richtungsselektivität der visuellen Divergenzgitter
Im visuellen Cortex V1 der Wirbeltiere beobachtet man eine Richtungsselektivität der sogenannten Orientierungssäulen. Dies sind Neuronengruppen, die sich durch alle sechs Schichten des visuellen Cortex ziehen und kleine zylinderförmige Säulen bilden. Deren Aktivität ist selektiv empfindlich auf den Neigungswinkel einer dunklen Linie vor hellem Hintergrund. Die beteiligten Neuronen müssen also auf dunkle Objekte ansprechen, sie sind daher vom Dunkel-On-Typ.
Wir analysieren zunächst die Reaktion einer magnocellularen Ganglienzelle der Retina vom Typ Dunkel-On, wenn über ihr rezeptives Feld eine dunkle Linie mit einem konstanten Anstellwinkel von links nach rechts bewegt wird. Die Linie wird quasi parallel zu sich selbst verschoben. Wir denken uns das rezeptive Feld der Ganglienzelle durch einen Kreis dargestellt. Jedes dunkle Objekt im Kreis wird eine Erregung der Ganglienzelle bewirken.
Für die Erkennung heller Linien auf dunklem Untergrund sind (nach Ansicht des Autors) die Hell-On-Ganglienzellen zuständig. Wir konzentrieren uns hier auf die Dunkel-On-Zellen.
Die Linie möge den Kreis schneiden, der das rezeptive Feld der Zelle darstellt, so dass ein Teil der Linie von ihr zur Sehne im Kreis wird. Die Länge dieser Sehne wird die Feuerrate der Ganglienzelle bestimmen. Wir gehen hier davon aus, dass die Erregung der Zelle mit dem Quadrat der Sehnenlänge zunimmt. Später können wir diese Voraussetzung möglicherweise wieder fallenlassen, wenn wir das Wirkprinzip der Orientierungssäulen begriffen haben. Zunächst interessieren wir uns nur für die Sehnenlänge.
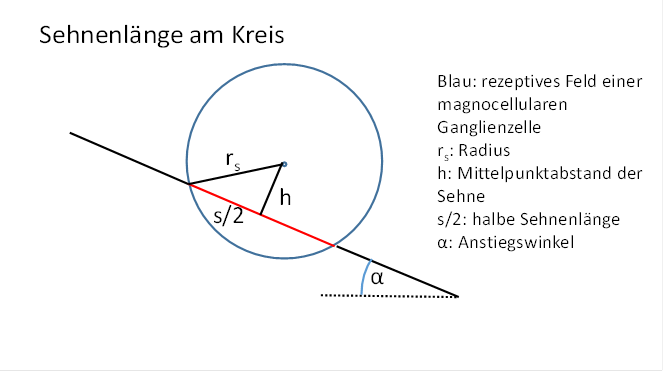
Abbildung 58 Sehnenlänge am Kreis
Die Sehnenlänge wird von der Lage der Geraden abhängen, genauer vom Abstand der Geraden zum Kreismittelpunkt.
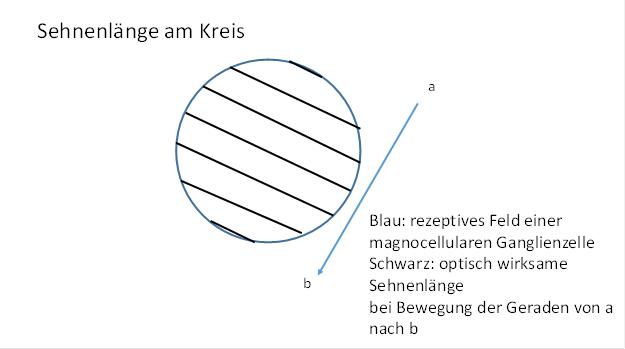
Abbildung 59- Sehnenlänge und Mittelpunktabstand
Eine geeignete Größe zur Berechnung der Sehnenlänge ist der Mittelpunktabstand der Sehne vom Kreismittelpunkt.
bildet die Hypotenuse eines rechtwinkligen Dreiecks, dessen Katheten h und die
halbe Sehnenlänge s/2 sind. Diese drei Größen sind über den Satz des Pythagoras
miteinander verknüpft.
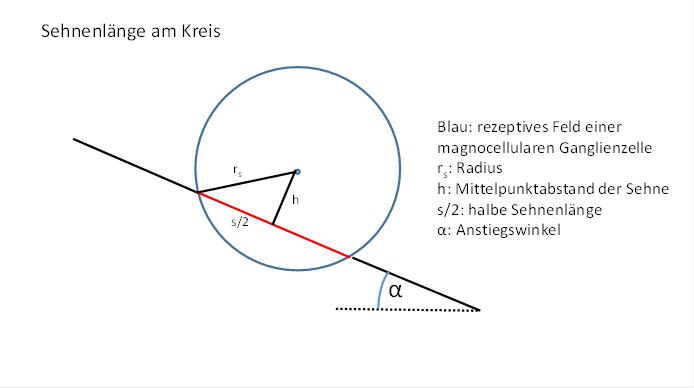
Abbildung 60- Berechnung der Sehnenlänge am Kreis
Es gilt also:
(Pythagoras)
Daraus ergibt sich für das Quadrat der Sehnenlänge folgende Gleichung:
Generell muss
gelten,
da r die Länge der Hypotenuse eines rechtwinkligen Dreiecks entspricht und h die
Länge einer Kathete darstellt. Anderenfalls wird das Quadrat der Sehnenlänge
negativ, also die Sehnenlänge eine imaginäre Zahl. Dann schneidet die Gerade den
Kreis nicht mehr, die Formel wird nicht mehr anwendbar.
Wir gehen hier davon aus, dass die Feuerrate f der Ganglienzelle, in deren rezeptiven Feld die Sehne mit der Länge s das Gesichtsfeld verdunkelt, quadratisch mit der Sehnenlänge zunimmt:
Wir betrachten nun die Sehnenlänge bzw. ihr Quadrat unter Verwendung eines Koordinatensystems, bei dem sich das rezeptive Feld nicht im Koordinatenursprung befindet. Der Mittelpunkt des Kreises K, der das rezeptive Feld der Ganglienzelle darstellen soll, möge im Koordinatensystem der Punkt Pk sein, dem wir die Koordinaten xm und ym zuordnen. Dann können wir den Punkt Pk auch als Pk(xm; ym) darstellen.
Die Gerade g, die den Kreis K schneiden möge, habe den Anstellwinkel φ zur x-Achse. Ihr Abstand vom Koordinatenursprung P(0;0) sei r.
Der Kreismittelpunkt Pk(xm; ym) möge vom Koordinatenursprung P(0; 0) den Abstand rk besitzen. Die Gerade, die beide Punkte verbindet, hat also die Länge rk. Sie möge mit der x-Achse den Winkel φk bilden.
Dann gilt für die Sehnenlänge sk die Gleichung
(4.2.1)
Zur Herleitung wird vorwiegend
der Satz des Pythagoras verwendet sowie die Darstellungen der Größen xm,
ym über den Sinus und Cosinus der Winkeldifferenz
.
Nützlich ist die grafische Darstellung der zur Herleitung nötigen Zusammenhänge
in nachfolgender Abbildung.
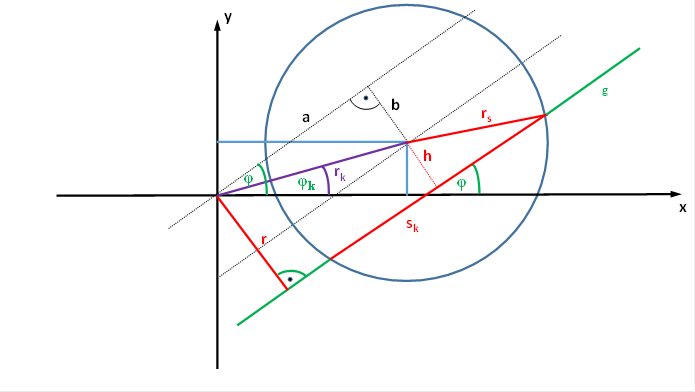
Abbildung 61- Sehnenlängenberechnung für ein verschobenes rezeptives Feld
Bezogen auf die obige Abbildung gilt:
Wir gehen davon aus, dass eine magnocellulare Dunkel-On-Ganglienzelle, deren rezeptives Feld von einer Geraden mit dem Anstiegswinkel φ und dem Abstand r vom Koordinatenursprung geschnitten wird, eine Feuerrate fk aufweist, die eine Funktion von φ und r darstellt.
(4.2.2)
Wir untersuchen nun die Feuerraten f12, f2, f3 und f4 von vier retinalen Ganglienzellen der beschriebenen Art unter der Vorgabe, dass diese im kartesischen Koordinatensystem genau entlang der Koordinatenachsen angeordnet sind und dabei einen Abstand r = 1 vom Koordinatenursprung besitzen. Dies ist in der folgenden Abbildung skizziert.
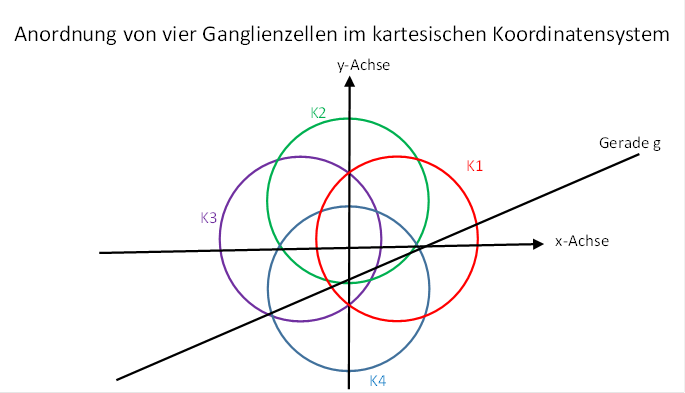
Abbildung 62- Anordnung von vier visuellen Ganglienzellen
Jede der vier Ganglienzellen habe bezüglich der Retina ein kreisförmiges rezeptives Feld mit dem Radius rs. Wichtig ist die teilweise oder völlige Überlappung der vier rezeptiven Felder. Die Gerade habe wieder den Anstiegswinkel φ.
Bei dieser Anordnung der Ganglienzellen gelten folgende Besonderheiten:
Damit vereinfachen sich die Formeln für die Feuerrate
der zugehörigen retinalen Ganglienzellen gemäß:
(4.2.3)
(4.2.4)
(4.2.5)
(4.2.6)
Diese vier Feuerraten gelangen von der Retina über das Corpus geniculatum laterale zum visuellen Cortex bzw. zur visuellen kranialen Wendeschleife, aus der er hervorging. Alle folgenden Betrachtungen beziehen sich nunmehr auf die Signalausbreitung dieser vier Inputsignale im visuellen Cortex. Die topologische Anordnung der vier Inputsignale möge dabei erhalten bleiben. Daher gibt es in visuellen Cortex vier Inputneuronen, die wiederum die Ecken eines Quadrates bilden und deren Feuerraten die Werte f1, f2, f3 und f4 gemäß unseren Formeln sind.
Die quadratische Fläche füllen wir mit Outputneuronen aus, die ihre Erregung über Interneuronen von den vier Inputneuronen beziehen. Vereinfacht können wir dazu das Quadrat durch gleichabständige waagerechte und senkrechte Gitterlinien unterteilen, in deren Schnittpunkten sich die Outputneuronen befinden mögen.
Wir wählen ein beliebiges Outputneuron aus und berechnen seine Erregung. Diese setzt sich aus vier Anteilen zusammen, denn es erhält von jedem der vier Inputneuronen einen Erregungsanteil. Allerdings tritt eine abstandsabhängige Dämpfung auf, bei der wir einen quadratischen Einfluss des Abstandes voraussetzen. Die Feuerrate des betrachteten Outputneurons genüge also der Gleichung
(4.2.7)
Die Feuerraten fk stammen von den beschriebenen retinalen Ganglienzellen.
Für die Abstände r1, r2, r3 und r4 des Outputneurons zu den vier Inputneuronen können wir ebenfalls geeignete Formeln herleiten. Dazu benötigen wir die nachfolgende Abbildung.
Wir beachten, dass die Inputneuronen gemäß unseren Vorgaben auf den Koordinatenachsen liegen und den Abstand 1 vom Koordinatenursprung besitzen.
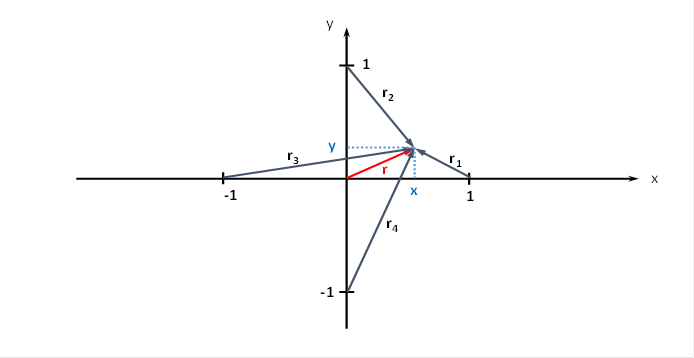
Abbildung 63- Radiusvektoren zu einem Neuron im Punkt P(x,y)
Spätestens hier wird deutlich, dass es sich auch in diesem Fall um ein ebenes Divergenzgitter handelt, für dessen Erregungsfunktion wir bereits die Formel (3.6) hergeleitet haben
(4.2.8)
In diese Gleichung müssen wir noch die hergeleiteten Formeln für die Feuerraten einsetzen, die von den retinalen Ganglienzellen des Typs Dunkel-On geliefert werden, wenn eine dunkle Linie mit einem Anstiegswinkel φ gesichtet wird.
Wenn eine geneigte Gerade im Sichtfeld der vier Ganglienzellen der Retina vorhanden ist, können wir die berechneten Feuerraten in diese Gleichung einsetzen und erhalten für die Gesamterregung f des betrachteten Outputneurons die Gleichung
(4.2.9)
Wir
rekapitulieren die allerwichtigsten Voraussetzungen: Das Outputneuron im Punkt
ist
ortsunveränderlich. Es kann sich
nicht aktiv bewegen. Daher sind die Parameter
und
konstant
und unveränderlich.
Weiterhin setzen wir voraus, dass der Anstiegswinkel φ der Geraden, die auch die rezeptiven Felder der vier retinalen Ganglienzellen überlagert, ebenfalls konstant bleibt.
Wenn nun die Gerade zu sich selbst parallelverschoben wird, ändert sich nur ihr Abstand r vom Koordinatenursprung. In diesem Falle wird im Experiment beobachtet, dass das Outputneuron genau dann maximal feuert, wenn der Anstiegswinkel der Geraden einen ganz bestimmten Wert annimmt. Benachbarte Outputzellen zeigen analog eine höhere Feuerrate, jedoch bei anderen Winkeln.
Mathematisch
bedeutet dies, dass die Feuerrate f der betrachteten Outputzelle im Punkt
eine
Funktion des Abstandes r darstellt und ein Maximum besitzt. Dies bedeutet, dass
die erste Ableitung von f nach r gleich null sein muss, während die zweite
Ableitung nach r negativ und ungleich null sein sollte. Genau dann hätte die
Erregungsfunktion f ein Maximum. Wir berechnen daher die erste und zweite
Ableitung nach r. Hierbei beachten wir, dass alle Größen mit Ausnahme von r
Konstante darstellen. Die erste Ableitung setzen wir gleich null.
(4.2.10)
Die zweite Ableitung nach r ergibt die einfache Gleichung
(4.2.11)
Damit erfüllt die zweite Ableitung die Bedingung für das Vorliegen eines Maximums, sie ist echt negativ kleiner Null.
Die durch Nullsetzen der
ersten Ableitung nach r entstandene Gleichung vereinfachen wir zunächst, indem
wir durch den gemeinsamen Faktor
dividieren.
Dies ist erlaubt, weil dieser Faktor ungleich null ist. So erhalten wir die
erste Vereinfachung:
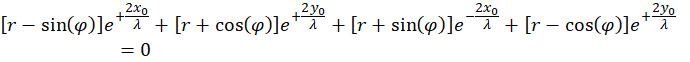
(4.2.12)
Vorteilhaft ist die Umformung in die Darstellung mit Hyperbelfunktionen.
Unter Verwendung dieser Beziehungen erhalten wir die Bedingung
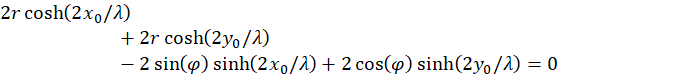
(4.2.13)
Damit haben wir eine Bedingung
für das Vorliegen eines Maximums der Erregungsfunktion f des Outputneurons im
Punkt
erhalten:
(4.2.14)
Diese Bestimmungsgleichung lässt sich nach dem Winkel φ auflösen. Hierzu verwenden wir die Formel
Mit
erhalten wir die Gleichung
(4.2.15)
Dies lässt sich umformen zu
(4.2.16)
Unter Beachtung von
ergibt
sich letztlich die gesuchte Bestimmungsgleichung für den Winkel φ, bei dem das
Outputneuron an der Stelle
seine
maximale Feuerrate f annimmt:
(4.2.17)
(4.2.18)
Für diesen Wert
von φ wird die Ableitung der Feuerrate f nach r gleich null, wobei die zweite
Ableitung kleiner als Null ist. Damit nimmt f ein lokales Maximum an. Hat also
die geneigte Gerade, die die rezeptiven Felder der vier beteiligten
Retina-Ganglienzellen scheidet, diesen Anstiegswinkel φ und den Abstand r vom
Koordinatenursprung, so feuert das Outputneuron im visuellen Cortex mit den
Koordinaten
an
stärksten und besitzt ein lokales Maximum. Genau dieses Verhalten zeichnet die
Neuronen der Orientierungssäulen im visuellen Cortex aus. Es beruht nicht auf
Lernvorgängen, sondern auf der Ausbreitung der Erregung benachbarter
magnocellularer Ganglienzellen im visuellen Cortex, wobei diese Ausbreitung
einer entfernungsabhängigen Dämpfung unterliegt. Wir hatten in unserem Modell
die quadratische Abhängigkeit der Feuerrate der Ganglienzellen von der Länge der
Sehne postuliert, ebenso die quadratische exponentielle Dämpfung. Dieses Modell
führte direkt auf eine Bestimmungsgleichung für den optimalen Winkel, bei dem
das stärkste Feuern des Outputneurons erfolgt. Andere Annahmen werden auf
analoge Resultate führen.
Wir nutzen nun die Möglichkeit, die Bestimmungsgleichung als Funktion von x und y darzustellen. Dann können wir z. B. in Excel den Zusammenhang zwischen dem Bestwinkel und dem Ort eines Outputneurons darstellen.
Zunächst sei im
Diagramm der konstante Teil
des
zweiten Summanden grafisch dargestellt:
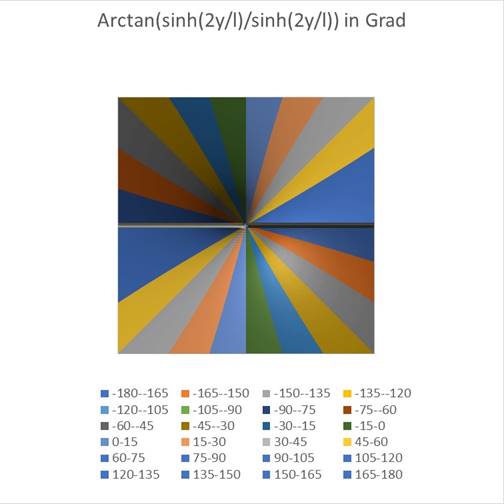
Abbildung 64- Die Winkelabhängigkeit des Terms T2
Dem dargestellten Winkel wurde im Abstand von 15 Grad jeweils eine andere Farbe zugewiesen (siehe Legende im Diagramm).
Hier wird sichtbar, welchen Beitrag der zweite Summand in der Bestimmungsgleichung für φ leistet. Dieser Beitrag ist unabhängig vom Abstand r der Geraden zum Koordinatenursprung.
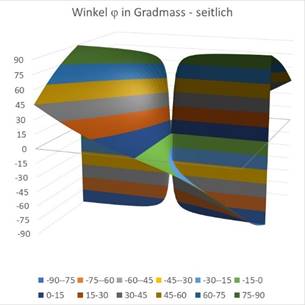
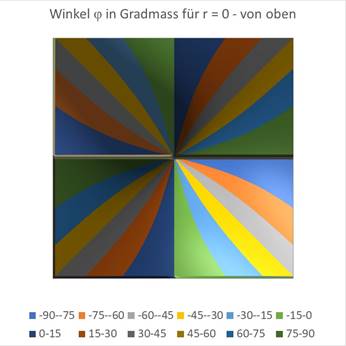
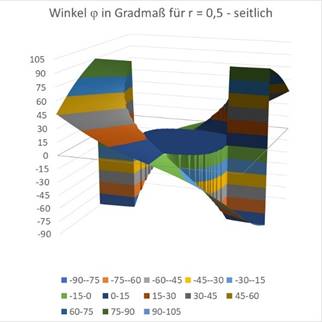
Die folgenden zwei Diagramme stellen den Winkel φ der Gesamtformel (18.5.3.21) dar in Abhängigkeit von den Werten x und y. Im linken Diagramm seitlich gesehen und daneben von oben. Zunächst wählen wir den Wert r = 0.
|
Abbildung 65- Darstellung des Winkels seitlich gesehen |
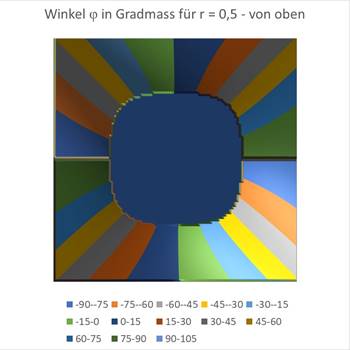
Abbildung 66- Darstellung des Winkels von oben gesehen |
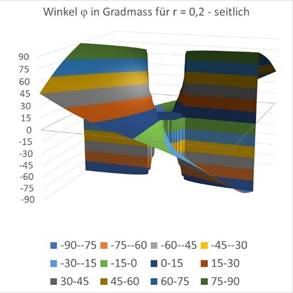
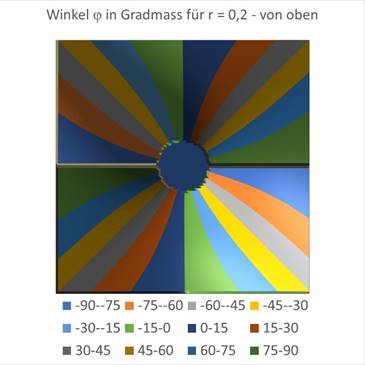
Den Einfluss des Radius r kann man ebenfalls grafisch darstellen. In der obigen Darstellung war r = 0 vorgegeben worden. Die Abbildungen sind Excel-Grafiken, bei denen die hergeleiteten Formeln für den Winkel φ zur Diagrammerstellung verwendet wurden. Für einen Wert von r = 0,2 erhält man die nachfolgenden Grafiken.
|
Abbildung 67- Der Einfluss von r auf die Richtungsselektivität |
Abbildung 68- Der Einfluss von r |
Hier sieht man, dass eine kreisähnliche kleine Umgebung des Koordinatenursprungs auf den Winkel φ = 0 anspricht, während in der übrigen Fläche die Winkel windmühlenartig angeordnet sind, wobei jedem Winkelintervall in Stufen von 15 Grad eine andere Farbe zugewiesen wurde. Genau dies wurde in den Experimenten zur Winkelselektivität der Orientierungssäulen im visuellen Cortex V1 ebenfalls so gehandhabt. In dieser Monografie wurde erstmals der mathematische Zusammenhang dargelegt.
Zuletzt die Grafiken für r = 0,5.
|
Abbildung 69- Orientierungssäulen für großes r |
Abbildung 70- Orientierungssäulen mit großem r |
Man sieht, dass der um den Koordinatenursprung befindliche Kreis, in dem auf einen Einfallswinkel von 0 Grad das Maximum vorliegt, größer wird, wenn r wächst. Etwa beim Wert von r = 0,7 ist die blaue Fläche bereits so groß, dass sie fast das gesamte Quadrat ausfüllt. Etwa ab diesem Wert reagieren die retinalen Ganglienzellen nicht mehr mit sinnvollem Output, da die geneigte Gerade die rezeptiven Felder nicht mehr genügend abdunkelt.
Der in Koordinatenursprung
befindliche blaue Kreis, dem der Neigungswinkel
zugeordnet
wird, stellt jedoch nicht die Fläche dar, in der die Outputneuronen beim Winkel
von 0 Grad am stärksten Feuern. Vielmehr ist an dieser Stelle der Funktionswert
des Winkels nicht definiert. Lediglich das Programm Excel von Microsoft ersetzt
den undefinierten Winkelwert durch den Zahlenwert 0, weil es wenigstens für die
übrigen Diagrammpunkte die
berechenbaren Winkelwerte bereitstellen will - so haben es die Programmierer von Excel entschieden. Diese Lösung ist weitaus besser als die Ausgabe hunderter Fehlermeldungen, die da lauten würden: -Funktionswert nicht definiert!-
Daher müssen wir an dieser
Stelle nachweisen, warum die Funktionswerte in dem blau dargestellten -Kreis-
nicht definiert sind. Gleichung (4.2.18) enthält den Term
.
Die Funktion arcsin(x) ist nur definiert für x-Werte im Intervall von -1 bis +1. Liegt x außerhalb dieses Intervalls, so gibt es keinen reellen Wert dieser Funktion arcsin(x). Excel gibt dann - vereinfacht - den Wert Null aus, weil Fehlermeldungen an dieser Stelle den Nutzer verwirren würden.
Eine Wertezunahme des
Parameters r im Term
führt
dazu, dass das Argument der Funktion für gewisse Parameterwerte außerhalb des
zulässigen Intervalls liegt. Je größer r wird, umso größer wird die Menge der
unzulässigen Werte.
Die Ursache ist einfach: Die Sehnenlänge muss nichtnegativ sein. Schneidet die geneigte Gerade den Kreis nicht mehr, so gibt es keine Sehnenlänge und die Formel verlässt den zulässigen Bereich.
Zusammenfassend könnte man formulieren:
Theorem der Richtungsselektivität der Orientierungssäulen im visuellen Cortex
Die Richtungsselektivität der Orientierungssäulen im primären visuellen Cortex und ihre Funktionsweise beruhen auf der Signalausbreitung in ebenen Divergenzgittern mit abstandsabhängiger, exponentieller Signaldämpfung. Diese Signaldivergenz erhöht primär die Redundanz und damit die Ausfallsicherheit des Systems, die Richtungsselektivität ist das Ergebnis der Signalausbreitung auf marklosen Fasern, bei der eine exponentielle Dämpfung auftritt. Letztere bewirkt die Richtungsselektivität.
Diese Richtungsselektivität ist übrigens unabhängig von einer Bewegung- insbesondere einer Parallelverschiebung der geneigten Linie. Lediglich der Mittelpunktabstand r der Linie zum Koordinatenursprung geht in die Formeln ein, der Anstellwinkel φ ist konstant. Und es zeigte sich, dass für jeden Anstellwinkel eine andere Population von Neuronen maximal feuert, und diese Populationen für verschiedene Anstellwinkel sind um das Zentrum windmühlenartig angeordnet, wie es in den Diagrammen zu sehen ist.
Das Besondere ist, dass ein ebenes Divergenzgitter keinerlei Lernvorgänge benötigt, seine Wirkprinzipien sind von Anfang an vorhanden. Damit erweist sich die Annahme, in den primären Cortexfeldern - die ihren Input nicht vom Spinocerebellum erhalten - wären lernfähige neuronale Netze vorhanden, als nicht notwendig. Die Richtungsselektivität wird nicht erlernt, sie ist von Anbeginn vorhanden. Sie beruht auf elementaren Naturgesetzen, insbesondere der exponentiellen Dämpfung von Erregungen beim Ausbreiten in der Fläche.
Dies erklärt, warum Nestflüchter sofort in der Lage sind, Objekte zu erkennen. Objekte werden zunächst erkannt durch die Wahrnehmung ihrer Umrisse, die als orientierte Linienelemente von den Orientierungssäulen im Cortex detektiert werden.
Wird die entfernungsabhängige Dämpfung nicht von einer Exponentialfunktion bewirkt, sondern von einer anderen Funktionenklasse, die ebenfalls konvex ist, so werden analoge Resultate erreicht. Insofern ist die als Kabelgleichung bezeichnete Funktion auch durch andere Funktionen ersetzbar.
- ← 5.5 Die Entstehung von Divergenzgittern im Cortex
- 5.7 Die Bildung von cortikalen Divergenzgittern im olfaktorischen Cortex →
Monografie von Dr. rer. nat. Andreas Heinrich Malczan