Theorie der neuronalen Schaltung des Gehirns

und des analytischen Denkens

ISBN 978-3-00-037458-6
ISBN 978-3-00-042153-2

Monografie von Dr. rer. nat. Andreas Heinrich Malczan

Teil 1.7. Die Erzeugung des (magnocellularen und primären) Kletterfasersignals zu einem Cortexcluster

Fassen wir zunächst unsere bisherigen Einsichten zusammen:

-          Die Großhirnrinde kann in Cortexcluster unterteilt werden.

-          In jedem Cortexcluster ermittelt ein magnocellulares Aktivitätsneuron die neuronale Clusteraktivität durch Mittelwertbildung über den übrigen Neuronen des Clusters.

-          Das Ausgangssignal des Aktivitätsneurons wird – falls es eine hinreichende und länger andauernde neuronale Clusteraktivität gibt, in einen neuronalen Systemtakt umgewandelt, der etwa eine Frequenz von 5 Hz besitzt.

-          Dieses Signal wird vom einem GABAergen Striosomenneuron – welches dem Cluster zugeordnet ist – über ein Axon zum Globus pallidus interna geleitet.

-          Der Globus pallidus interna ist ein negativer Negationskern mit externer Einssignalbildung. Sein zur Negation erforderliches erregendes Einssignal bezieht er vom Nucleus subthalamicus. Dieses Einsignal erregt ein GABAerges Outputneuron dauerhaft.

-          Genau dieses dauererregte Outputneuron wird vom eintreffenden Output des GABAergen Striosomenneurons stark gehemmt, wenn der Systemtakt im neuronalen Schwingkreis gerade den Wert 1 annimmt. Anderenfalls unterbleibt die starke Hemmung.

-          Daher ist der Output des zugehörigen Neurons des Globus pallidus interna der negierte neuronale Systemtakt.

-          Dieser Output erreicht als Input den Nucleus ruber. Dieser ist ein positiver Negationskern. Er bildet sein erregendes Einssignals selbst aus dem ihm zugeführten Input vom Cortex, der unter anderem die ursprünglichen Mittelwertsignale aller Clusterneuronen enthält. Dieses Dauersignal wird vom zugehörigen Neuron des Globus pallidus gehemmt. Dadurch wird der Output des Globus pallidus negiert. Als Ergebnis entsteht der doppelt negierte neuronale Systemtakt des neuronalen Elementarschwingkreises.

-          Dieser doppelt negierte Systemtakt aus dem zugehörigen Striosomenneuron wird letztendlich im Nucleus olivaris inferior auf den Transmitter Glutamat/Aspartat umgeschaltet und erreicht als Kletterfasersignal sowohl die Kleinhirnkerne als auch eine zugeordnete Purkinjezelle.

Damit gilt das nachfolgende Theorem, welches der Autor zu Ehren der Hauptstand Deutschlands als Berliner Theorem bezeichnet.

Theorem 1.15: Berliner Theorem

Jeder Cortexcluster generiert unter Zuhilfenahme des Striosomensystems der Basalganglien, der Substantia nigra pars compacta, des Globus pallidus pars interna, des Nucleus ruber und des Nucleus olivaris inferior ein magnocellulares primäres Kletterfasersignal, falls die Clusteraktivität einen Schwellwert übersteigt.

Es erscheint nötig, dem Neuron im Nucleus ruber bzw. im Nucleus olivaris, dessen Axon das primäre magnocellulare Kletterfasersignal zum Cerebellum transportiert, einen eigenen Namen zu geben.

Definition 1.19: Primäres Kletterfaserneuron

Das Neuron im Nucleus olivaris inferior, dessen Axon das primäre magnocellulare Kletterfasersignal zum zugeordneten Cerebellumcluster sendet, bezeichnen wir als primäres Kletterfaserneuron des Nucleus olivaris inferior.

Das Neuron des Nucleus ruber, dessen Axon das primäre Kletterfaserneuron im Nucleus olivaris inferior mit Input versorgt, bezeichnen wir als primäres Kletterfaserneuron des Nucleus ruber.

Wenn der Autor dieses magnocellulare Kletterfasersignal als primäres bezeichnet, so ist davon auszugehen, dass es offenbar auch sekundäre Kletterfasersignale gibt. Diese werden durch einen speziellen Algorithmus vom primären Kletterfasersignal abgeleitet. Damit klärt sich auch das Problem, dass es in jedem Cerebellumcluster sehr viele Purkinjezellen gibt, denen zunächst nur ein primäres Kletterfasersignal zur Verfügung steht. Die erste Purkinjezelle bzw. Purkinjegruppe ist dem primären Kletterfasersignal zugeordnet, die übrigen erhalten ein sekundäres Kletterfasersignal. Doch dazu später.

Es darf vermutet werden, dass das Kletterfasersignal zur Abspeicherung der gerade aktuellen Signalkombination im Cortexcluster dient. Im Vorgriff auf spätere Ausführungen werden wir das in der Purkinjezelle abgespeicherte Signal als das Eigensignal der Purkinjezelle bezeichnen. Damit aber ein Cortexsignal überhaupt zum Eigensignal einer Purkinjezelle werden kann, ist es jedoch erforderlich, dass die Signale der beteiligten Signalneuronen des Cortexclusters einen Weg zum Cerebellum finden. Dies ist tatsächlich der Fall.

Theorem 1.16: Projektion der Signalneuronen eines Cortexclusters in das Cerebellum

Die Signalneuronen eines jeden Cortexclusters projizieren erregend ins Cerebellum. Jedes Signalneuron projiziert zunächst über die Brückenkerne zu den Kleinhirnkernen, wo es über Kollateralen erregend auf die Outputneuronen der Kleinhirnkerne wirkt. Weiterhin projiziert jedes Signalneuron über eine Moosfaser ins Cerebellum. Die Moosfasern aller Signalneuronen eines Clusters bilden über die Moosfaserprojektion letztlich eine Schaar von Parallelfasern in ein Cerebellum-Teilgebiet, welches in dieser Theorie als zugehöriges Cerebellumcluster bezeichnet wird. Alle Purkinjezellen, die diese gemeinsame Parallelfaserpopulation inputmäßig anzapfen, bilden ein Cerebellumcluster von Purkinjezellen. Alle Purkinjezellen des Cerebellumclusters werden also über die gemeinsame Schaar von Parallelfasern genau von dem Output aller Signalneuronen des zugehörigen Cortexclusters erreicht. Somit entspricht jedem Cortexcluster ein zugeordnetes Cerebellumcluster.

Hinweis: Cerebellumcluster werden in der englischsprachigen Wikipedia bereits beschrieben (Stand Juni 2011). Neu hinzugefügt wurde vom Autor dieser Monografie die Hypothese, dass das Mittelwertneurons eines Cortexclusters genau dann ein primäres Kletterfasersignal für das zugeordnete Cerebellumcluster generiert, wenn die Signallage im Cortexcluster hinreichend aktiv ist. Weiterhin postuliert der Autor, dass die Signalneuronen des Cortexclusters genau in dieses Cerebellumcluster projizieren. Dadurch postuliert der Autor die Existenz einer topologischen Abbildung der Cortexcluster auf die Cerebellumcluster. In diese topologische Abbildung sind sowohl die Signalneuronen als auch die Aktivitätsneuronen des Cortexclusters einbezogen.

Bekanntlich sind die Outputneuronen der Kleinhirnkerne (bis auf wenige Ausnahmen) die einzige Ausgangsstation des Cerebellums. Aber die Kleinhirnkerne geben nicht nur den Cerebellum-Output aus, sondern empfangen über Axonkollateralen auch den Input der Moos- und Kletterfasern. Daher erscheint es überaus angebracht, den Aufbau und die Funktionsweise der Kleinhirnkerne aus cytoarchitektonischer Sicht näher zu beleuchten.

In der Dissertation von Susanne Kamphausen über die „Funktionelle Architektur der Kleinhirnkerne der Ratte“ werden die Fakten genannt:

·         Es gibt (bei der Ratte) zwei Arten von Projektionsneuronen in den Kleinhirnkernen

·         Erstens große, exitatorische Projektionsneurone mit fusiformen bzw. multipolaren Somata, 15 - 35 µm groß, 2 bis 5 primäre Dendriten, dornig oder glatt, Transmitter Glutamat, sie projizieren in Motorzentren des Hirnstammes, des Mesencephalon, in den Thalamus und die Vestibularkerne

·         Zweitens mittelgroße GABAerge Projektionsneurone, sie innervieren vorwiegend die inferiore Olive (93%), aber auch den cerebellaren Cortex oder die Brücke, 5 – 20 µm, fusiforme oder multipolare Somata

·         Drittens existieren lokale, inhibitorische Neuronen 5 – 15 µm, Transmitter GABA oder/und Glycin

Weiter lesen wir in dieser Dissertation sinngemäß:

·         Einzelne Purkinjezellen bilden sowohl mit glutamatergen als auch mit GABAergen Projektionsneuronen Synapsen aus.

·         Das Verhältnis Purkinjezellen zu Neuronen der Kleinhirnkerne wurde auf 10:1 geschätzt.

(Ende der nichtwörtlichen Wiedergabe aus oben genannter Dissertation)

Wie haben wir uns die Schaltung der Kleinhirnkerne nun vorzustellen? Offenbar gibt es in den Kleinhirnkernen sowohl positive als auch negative Einssignalneuronen. Beide beziehen ihre Erregung aus dem Input der Moosfasern und Kletterfasern. Beide Arten von Einssignalneuronen sind Projektionsneuronen, die einen glutamaterg und die anderen GABAerg. Beide Arten von Einssignalneuronen werden jeweils von der zugeordneten Purkinjezelle standardmäßig stark gehemmt. Nur wenn eine Purkinjezelle ihr Eigensignal wiedererkennt, fällt diese Hemmung aus und die entsprechenden Signale ziehen zu den Zielorten. Das glutamaterge, also erregende Signal zieht zum Thalamus (und von dort zum Cortex), das hemmende zur Olive.

In dieser Arbeit wurde bereits gezeigt, dass der Nucleus subthalamicus ein positiver Einssignalkern ist. Seine Einssignalneuronen bilden ihre Einssignale durch erneute Mittelwertbildung aus den Signalen der cortikalen Mittelwertsignale aus der Schicht V des Cortex.

Es ist erstaunlich, dass das Prinzip der Einssignalbildung auch in den Cerebellumkernen angewendet wird. Noch interessanter ist, dass es dort sowohl positive, also erregende Einssignale gibt als auch negative, also hemmende.

Der zur Einssignalbildung erforderliche Input strömt einerseits über die Kollateralen der Moosfasern in den Cerebellumkern, andererseits über die Kollateralen der Kletterfasern. (Später wird sich zeigen, dass jedes Kernneuron nur von einer Kletterfaser kontaktiert wird, während alle Moosfasern eines Clusters jedes Kernneuron mit Input beliefern).

Nun bringt ein reines Einssignal, also ein neuronales Dauersignal – egal ob hemmend oder erregend – noch keinerlei Erkenntnisgewinn. Aber es bildet die Voraussetzung für eine Outputerzeugung durch Negation beziehungsweise Invertierung. Bei der Negation wird das Einssignal vom hemmenden Input total unterdrückt und führt so zur Negation des Inputs. Bei der Invertierung ist die Hemmung durch den Input unvollkommen und hängt in ihrer Hemmungsstärke von der Feuerrate des hemmenden Inputs ab. Bei der Invertierung bleibt also nach der Hemmung des Einssignals noch ein Restsignal übrig, dessen Feuerrate etwa indirekt proportional zur ursprünglichen Signalstärke des hemmenden Inputs ist, wenn man Linearität voraussetzt.

Wir postulieren also zunächst einmal die Existenz der positiven und negativen Einssignalneuronen in den Cerebellumkernen.

Theorem 1.17: Positive und negative Einssignalneuronen in den Cerebellumkernen

In den Cerebellumkernen existieren glutamaterge Outputneuronen, die als positive Einssignalneuronen wirken. Ihre Einssignalerregung wird erzeugt durch den erregenden Input der Kollateralen der Moos- und Kletterfasern. Ihr positives Einssignal wird von den zugeordneten Purkinjezellen gehemmt, wodurch eine Invertierung des Purkinjeoutputs erzeugt wird. Die positiven Einssignalneuronen der Cerebellumkerne projizieren erregend vorwiegend in die Motorzentren des Hirnstammes, des Mesencephalon, in den Thalamus und die Vestibularkerne

Ebenso existieren in den Cerebellumkernen GABAerge Outputneuronen, die als negative Einssignalneuronen wirken. Ihre Einssignalerregung wird erzeugt durch den erregenden Input der Kollateralen der Moos- und Kletterfasern. Ihr negatives Einssignal wird von den zugeordneten Purkinjezellen gehemmt, wodurch eine Invertierung des Purkinjeoutputs erzeugt wird. Die negativen Einssignalneuronen der Cerebellumkerne projizieren hemmend vorwiegend in die inferiore Olive (93%), aber auch in den cerebellaren Cortex oder in die Brücke. Ab einer gewissen evolutionären Entwicklungsstufe projizieren sie ebenfalls hemmend in den Nucleus ruber.

Zu jedem positiven Einssignalneuron der Cerebellumkerne gibt es einen Partner unter den negativen Einssignalneuronen, der mit der gleichen Gruppe von Purkinjezellen hemmend verbunden ist.

Zur Verkürzung künftiger Texte werden wir den erregenden und den hemmenden Outputneuronen der Kleinhirnkerne einen eigenen Namen geben.

Definition 1.20: Positive und negative Kernneuronen

Die glutamatergen Outputneuronen der Kleinhirnkerne werden wir als positive Kernneuronen bezeichnen, die GABAergen Outputneuronen der Kleinhirnkerne als negative Kernneuronen.

Es wäre höchst erfreulich, wenn sich die neurologische Fachwelt darauf verständigen könnte, dass (ab einer gewissen Entwicklungsstufe) neben der hemmenden Projektion zur Olive eine ebenfalls hemmende Projektion zum Nucleus ruber erfolgt (weil z. B. das hemmende Projektionsaxon sich teilt und eine Kollaterale zur Olive, die zweite zum Nucleus ruber zieht). Diese ist spätestens seit der Verarbeitung des Brückenkernoutputs durch das Cerebellum aus systemtheoretischer Sicht dringend vonnöten. Daher wird diese GABAerge Projektion aus dem Nucleus dentatus zum Nucleus ruber erst bei höher entwickelten Säugetieren auftreten, während sie bei den niederen fehlt. Vielleicht ist dies der Grund für die einander widersprechenden Angaben in der Fachliteratur. Die genau in dieser Fachliteratur anzutreffende Vermutung, der Nucleus ruber sei eine Art „Umschaltkern“, der bei Bedarf zwischen Cerebrum und Cerebellum umschalte, könnte durch eine hemmende Projektion vom Nucleus dentatus zum Nucleus ruber sogar wissenschaftlich bewiesen werden. Auch könnte dann nachgewiesen werden, was denn da eigentlich umgeschaltet wird und wozu, und vor allem wie dies erfolgt. Daher ist die zweifelsfreie Existenz dieser hemmenden Verbindung so wichtig.

Da es nach allgemein bekannter Ansicht jeweils mehrere Purkinjezellen auf jeweils ein erregendes bzw. hemmendes Outputneuron der Cerebellumkerne projizieren, wollen wir diesen Purkinjezellen einen eigenen Namen geben.

Definition 1.21: Purkinjegruppe

Alle Purkinjezellen, die mit ihrem hemmenden Output gemeinsam sowohl auf das gleiche positive Kernneuron projizieren als auch ebenso gemeinsam auf das gleiche negative Kernneuron projizieren, nennen wir eine Purkinjegruppe.

Eine Purkinjegruppe besteht mindestens aus einer Purkinjezelle. Sie kann aber auch größere Anzahl von Purkinjezellen umfassen, zum Beispiel drei, acht oder gar dreizehn Purkinje-zellen. Die reale Anzahl der Purkinjezellen einer Purkinjegruppe hängt von der evolutionären Entwicklungsstufe des Lebewesens und von dem Typ des Kleinhirnkerns ab. Die verschiede-nen Kleinhirnkerne ein- und desselben Lebewesens repräsentieren ebenfalls unterschiedliche evolutionäre Entwicklungsstufen. Offenbar entstanden sie durch Duplikation, also einfache Verdoppelung. Da danach der neu entstandene (verdoppelte) Partnerkern noch keine Aufgaben hatte, konnte er sich durch Modifikation seiner Cytoarchitektur weiterentwickeln und ein höheres systemtheoretisches Niveau erreichen. Die höchste Entwicklungsstufe unter den Kleinhirnkernen besitzt der Nucleus dentatus.

Unbestritten ist in der neuronalen Fachwelt die Tatsache, dass eine einzelne Kletterfaser durchaus mehrere Purkinjezellen innervieren kann. Dazu teilt sie sich auf. Auch hier schwanken die Literaturangaben zwischen einer einzigen Purkinjezelle, andere geben drei, weitere Quellen acht bis 13 Purkinjezellen an, die von der gleichen Kletterfaser versorgt werden. Der Autor postuliert daher, dass diejenigen Purkinjezellen, die ihren Output an die gleichen Outputneuronen des Kleinhirnkerns senden, auch von der gleichen Kletterfaser erregt werden. Diese Purkinjezellen bilden aber nach obiger Definition eine Purkinjegruppe. Daher gelte nachfolgendes Theorem:

Theorem 1.18: Jeder Purkinjegruppe ist genau eine Kletterfaser zugeordnet und umgekehrt

Jede Kletterfaser innerviert immer nur die Purkinjezellen genau einer Purkinjegruppe des Cerebellumclusters sowie das zugehörige erregende und das zugehörige hemmende Einssignalneuron des Cerebellumkerns (Kernneuron). Verschiedene Purkinjegruppen benutzen verschiedene Kletterfasern.

Zwischen den verschiedenen Kletterfasern und den Purkinjegruppen gibt es also eine eineindeutige Abbildung. Es gibt (etwa) so viele verschiedene Kletterfasern wir Purkinjegruppen.

Welche Bedeutung die Zusammenfassung mehrerer Purkinjezellen zu einer Purkinjegruppe hat, wird nachfolgend geklärt werden.

Bekannterweise hat jede Purkinjezelle eine Kletterfaserleitung. Auch wenn sich nun vielleicht drei, acht oder sogar bis zu dreizehn Purkinjezellen eine gemeinsame Kletterfaser teilen und eine Purkinjegruppe bilden, so ist doch zunächst unklar, woher die vielen Kletterfasern kommen sollen.

Bisher wurde nur gezeigt, dass pro Cortexcluster genau ein Aktivitätsneuron existiert, aus dessen Signal das Striosomensystem der Basalganglien durch Rückkopplung und doppelte Negation genau ein primäres Kletterfasersignal erzeugt. Dieses einzige Mittelwert-Kletterfasersignal jedes Cortexclusters kann nun genau an einer und nur einer Purkinjegruppe andocken und sie mit Input versorgen. Diese spezielle Purkinjegruppe wollen wir für die spätere Klassifizierung bereits jetzt mit einem speziellen Namen versehen.

Definition 1.22: Startgruppe und primäres magnocellulares Kletterfasersignal

Die Purkinjegruppen eines Cerebellumclusters sind entlang des Moosfaserstranges dieses Cerebellumclusters nacheinander angeordnet. Diejenige Purkinjegruppe, die am Anfang dieses Moosfaserstranges als erste angeordnet ist, nennen wir die Startgruppe des zugehörigen Cerebellumclusters. Das zugehörige Kletterfasersignal bezeichnen wir als primäres magnocellulares Kletterfasersignal, das entsprechende Axon als primäre magnocellulare Kletterfaser.

Alle übrigen Purkinjegruppen erhalten ihr Kletterfasersignal über einen anderen Algorithmus, der noch zu erläutern sein wird. Wir werden sie als sekundäre (magnocellulare) Kletterfasersignale bezeichnen.

Die evolutionäre Ursache für die Existenz von primären und sekundären Kletterfasersignalen liegt in der fortschreitenden Entwicklung des Cerebellums. Anfangs gab es nur eine Purkinje-zelle pro Cortexcluster. Später kamen eine zweite, eine dritte und eine vierte hinzu. Alle diese hinzukommenden Purkinjezellen speicherten anfangs genau das gleiche Signal. Dies war zunächst sinnvoll. Beim neuronalen Tod einer Purkinjezelle blieb das System arbeitsfähig. Daher waren die „überzähligen“ Purkinjezellen einer Purkinjegruppe sozusagen die „eiserne Reserve“. Sie bildeten eine Purkinjegruppe, die auch zugleich die Startgrupppe war.

Später kamen weitere Purkinjegruppen hinzu, die als Reservezellen eigentlich nicht nötig waren. Etwa zu dieser Zeit mögen die Golgi-Zellen an Bedeutung gewonnen haben. Ebenso erfuhren die Olive und der Nucleus ruber eine cytoarchitektonische Erweiterung. Diese bestand in der Nutzung der GABAergen Projektion aus den Cerebellumkernen zur Erzeugung eines neuen, des sekundären Kletterfasersignals.

Dieses sekundäre Kletterfasersignal wurde durch einen neu entwickelten Algorithmus gebildet. Er ermöglichte es, dass die zweite Purkinjegruppe ein anderes Signal speichern konnte als die erste Gruppe, die zugleich die Startgruppe war. Und später konnte die neu hinzugekommene dritte Gruppe ein weiteres, ein drittes Signal speichern. Im modernen Cerebellum speichert also jede Purkinjegruppe ein neues, von den bisherigen gespeicherten Signalen völlig verschiedenes Signal ab.

Die eigentliche systemtheoretische Aufgabe einer Purkinjegruppe besteht im Erlernen und im Wiedererkennen eines Signals, welches als Input vom Cortex über die Brückenkerne und die Moosfasern in die Parallelfasern einströmt und erlernt bzw. wiedererkannt wird.

Hierbei gibt es zwei Varianten:

-          Das Signal wurde erkannt. Dann erfolgte aus dem Cerebellumkern eine erregende Projektion zum Thalamus und eine hemmende zur Olive und evtl. auch zum Nucleus ruber.

-          Das Signal wurde nicht erkannt. Dann gab es (fast) keinen Output aus dem Cerebellumkern.

Nach Ansicht des Autors bewirkt die hemmende Projektion des Cerebellumkern-Neurons zur Olive die Unterdrückung des Kletterfasersignals. Denn dieses Neuron feuert nur dann, wenn die Purkinjegruppe ihr gespeichertes Eigensignal erkennt. Genau in diesem Moment wird mit dem Output des negativen Kernneurons das vorhandene Kletterfasersignal unterdrückt, solange das Eigensignal an der Purkinjegruppe anliegt.

Da das Kletterfasersignal den neuronalen „Schreibbefehl“ darstellt, wird das Kletterfasersignal nunmehr unterdrückt und dadurch daran gehindert, eine andere, weitere (und freie) Purkinjegruppe zu prägen. Erst dadurch konnten die verschiedenen Purkinjegruppen verschiedene Signale erlernen. Denn ein bereits erlerntes Signal führte immer dann, wenn es an den Parallelfasern anlag und von der Purkinjezelle erkannt wurde, sofort zur Hemmung des Kletterfasersignals. So wurden weitere „Lernvorgänge“ mit dem bereits erlernten Signal verhindert.

Der hemmende Output des negativen Kernneurons zur Olive diente jedoch nicht nur der Hemmung des primären Kletterfasersignals. Das Fehlen dieser Hemmung diente auch  der Erzeugung des sekundären Kletterfasersignals.

Für die Erzeugung der sekundären Kletterfasersignale entwickelte die Evolution (nach Ansicht des Autors dieser Monografie) zwei Verfahren.

Das evolutionär ältere Verfahren bestand darin, dass es ein genau zentrales Kletterfaserneuron pro Cerebellumcluster im Nucleus olivaris gab. Von diesem wurden durch zentrale Verteilung alle sekundären Kletterfasersignale abgeleitet. Jede Purkinjegruppe erhielt also über eine Axonkollaterale genau den Output des zentralen Kletterfaserneurons. Jede Purkinjegruppe sandte das hemmende Axon des negativen Kernneurons aus dem Kleinhirnkern genau zu diesem zentralen Kletterfaserneuron und hemmte dessen Erregung immer genau dann, wenn diese Gruppe ihr Eigensignal erkannte. So konnte dieses zentrale Kletterfaserneuron nur dann feuern, wenn es vom Mittelwertneuron des Cortexclusters stark erregt wurde und keine der bereits geprägten Purkinjegruppen dieses Signal als ihr Eigensignal erkannte. Dadurch wurde sichergestellt, dass nur unbekannte Signale als neue Signale abgespeichert wurden.

Skizze 1.20: Zentrale Verteilung des Kletterfasersignals (evolutionär älteste Variante)

 

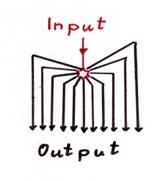
Hinweis: In obiger Skizze ist nur die Verteilung des Outputs des zentralen Kletterfaserneurons der Olive dargestellt, es fehlen sämtliche hemmenden Leitungen von den negativen Kernneuronen zu genau dem einzigen Zentralneuron.

Theorem 1.19: Gewinnung der sekundären Kletterfasersignale aus dem primären Kletterfasersignal durch zentrale Verteilung in der Olive

Im Falle der zentralen Verteilung des Kletterfasersignals erregt das primäre Kletterfasersignal des Cortexclusters genau ein zentrales Kletterfaserneuron der Olive, von dem sämtliche Purkinjegruppen ihr Kletterfaseraxon beziehen. Somit wären zunächst alle Kletterfaseraxone immer synchron erregt. Aber das negative Kernneuron einer jeden Purkinjegruppe hemmt dieses zentrale Kletterfaserneuron genau dann, wenn es selbst aktiv ist, so dass dann alle Kletterfaseraxone gleichzeitig signallos sind.

Die zweite Variante der Erzeugung der sekundären Kletterfasersignale aus dem primären Kletterfasersignal war die sequentielle Verteilung. Sie ging aus der zentralen Verteilung hervor, als die Anzahl der Purkinjegruppen zu groß wurde, um von einem einzigen Zentralneuron der Olive beherrscht zu werden. Nunmehr wurde das Kletterfasersignal in einer Neuronenkette weitergereicht, an deren Anfang sich das primäre Kletterfaserneuron befand. Daher hemmte jede Purkinjegruppe im Erkennungsfalle mit ihrem negativen Kernneuron das Kletterfaserneuron der benachbarten Purkinjegruppe, so dass deren Prägung unmöglich war, wenn die Vorgängergruppe das anliegende Signal erkannt hatte.

Skizze 1.21: Sequentielle Verteilung des primären Kletterfasersignals (mittlere evolutionäre Stufe)

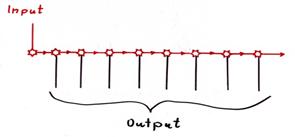
Hinweis: In obiger Skizze ist nur die sequentielle Verteilung des Outputs des primären Kletterfaserneurons der Olive dargestellt, es fehlen sämtliche hemmenden Leitungen von den negativen Kernneuronen zu den Verteilungsneuronen. Die Weitergabe des Outputs erfolgt hier nicht zentral, sondern mit Hilfe von erregenden Interneuronen oder über Axonkollateralen in einer Kette.

Theorem 1.20: Erzeugung der sekundären, magnocellularen Kletterfasersignale durch sequentielle Verteilung in der Olive

Der Output des negativen Kernneurons der Startgruppe unter den Purkinjegruppen hemmt das primäre Kletterfaserneuron im Nucleus olivaris inferior.

Der Output dieses primären Kletterfaserneurons der Olive okkupiert ein freies Neuron in der Olive und erregt es mit seinem Output. Dieses okkupierte Neuron liefert das Kletterfasersignal für die benachbarte Purkinjegruppe der Startgruppe.

Der Output des k-ten negativen Kernneurons der k-ten Purkinjegruppe hemmt das Kletter-faserneuron dieser Purkinjegruppe. Dieses Kletterfaserneuron ist das k-te Kletterfaserneuron des zugehörigen Cerebellumclusters. Der Output dieses k-ten Kletterfaserneurons der Olive ist der Input für das (k+1)-te Kletterfaserneuron der Olive, welches die Nachbar-gruppe der k-ten Purkinjegruppe, also die (k+1)-te Purkinjegruppe mit Kletterfaserinput versorgt.

Dieser Prozess der Bildung des Kletterfaserinputs für die benachbarte Purkinjegruppe setzt sich solange fort, bis alle Purkinjegruppen des Cerebellumclusters aufgebraucht sind und sich keine neuen mehr bilden können. Ebenso kommt dieser rekursive Prozess zum Erliegen, wenn die entsprechenden Neuronen in der Olive aufgebraucht sind.

Auch hier sind zunächst einmal alle Kletterfaseraxone synchron erregt, bis eine Purkinjegruppe ihr Eigensignal erkennt und ihr negatives Kernneuron hemmend auf die zuführende Kletterfaser wirkt. Alle nachfolgenden Kletterfasern werden dadurch ebenfalls signallos.

Skizze 1.22: Erzeugung der sekundären Kletterfasersignale durch sequentielle Verteilung in der Olive und rekurrente Hemmung des Verteilungsneurons durch das negative Kernneuron

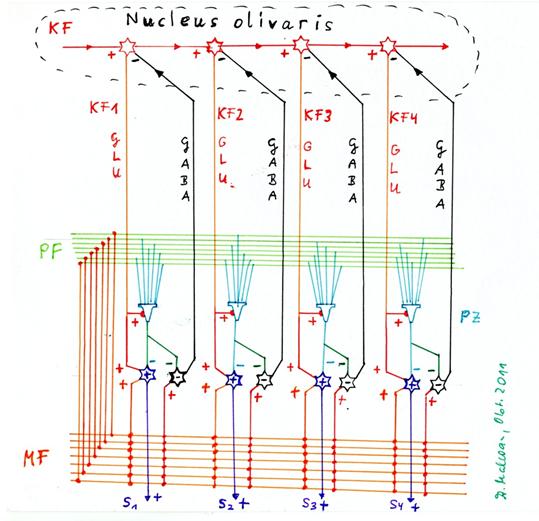
Eingezeichnet in obiger Skizze sind vier Purkinjezellen, zu jeder das positive (+) sowie negative (-) Kernneuron, die Moosfasern, die Parallelfasern, das primäre Kletterfaseraxon KF, die vier Verteilungsneuronen für das Kletterfasersignal im Nucleus olivaris sowie die hemmende Projektion eines jeden negativen Kernneurons zum zugehörigen Verteilungsneuron für das Kletterfasersignal im Nucleus olivaris. Nicht eingezeichnet sind Sternzellen, Korbzellen und Golgizellen, da es hier nur um die Erzeugung der sekundären Kletterfasersignale geht.

Nun ist die Hemmung des Kletterfasersignals im Falle der Signalerkennung eine wichtige notwendige Voraussetzung, aber noch keine Garantie dafür, dass nicht alle Purkinjegruppen eines Cerebellumclusters mit dem gleichen Prägungssignal geprägt werden. Theoretisch wäre es durchaus denkbar, dass alle Purkinjegruppen, ja alle Purkinjezellen in einem Ritt mit dem gleichen Signal geprägt werden könnten.

Genau dies aber muss in der Realität verhindert werden. Es reicht schließlich aus, wenn innerhalb einer Purkinjegruppe alle Zellen das gleiche Signal speichern und dadurch eine Ausfallversicherung gegen den neuronalen Tod einzelner Purkinjezellen vorhanden ist. Die Prägung aller Purkinjegruppen mit dem gleichen Signal wäre eine ungeheure Verschwendung an Ressourcen.

Nach diesen Darlegungen muss das Augenmerk deshalb auf die Golgizellen des Cerebellums gelegt werden. In der neuronalen Fachliteratur fehlte bis zum Erscheinen dieser Monografie eine (plausible) systemtheoretische Begründung für die Existenz der Golgi-Zellen des Cerebellums. Unstrittig ist eine gewisse Kontrastverstärkung, die vermutet wird. Mehr Erkenntnisse liegen bisher jedoch nicht vor.

Daher sammeln wir zunächst die Fakten zum Thema Golgizellen. Im Lehrbuch „Anatomie Band 4“ von Graumann/Sasse lesen wir auf Seite 279 wörtlich:

 

(Zitatbeginn:)

 

„Golgi-Zellen sind große hemmende Interneurone. Sie liegen sparsam verteilt im Stratum granulosum, haben aber einen sich in alle Richtungen des Raumes weit verzweigenden Dendritenbaum. Sie kontrollieren die Aktivität der Körnerzellen.“

 

                                                                                                                      (Zitatende)

 

Es ist also davon auszugehen, dass es deutlich weniger Golgizellen als Purkinjezellen gibt.

Wenn es nun einerseits deutlich weniger Golgizellen als Purkinjezellen gibt, andererseits die Purkinjezellen Gruppen bilden, die von der gleichen Kletterfaser angesteuert werden und deren Output auf ein positives und ein negatives Einssignalneuron des Cerebellumkerns konvergiert, so gibt es nur eine vernünftige Erklärung: Jeweils eine Purkinjegruppe bildet mit genau einer Golgizelle eine Einheit. Dann müsste es etwa genauso viele verschiedene Kletterfasern geben wie Golgizellen. Ebenso müsste die Anzahl der Golgizellen in etwa der Anzahl der positiven bzw. negativen Einssignalneuronen in den Kleinhirnkernen entsprechen.

Wir gehen bereits jetzt davon aus, dass diese Kriterien in etwa zutreffen und formulieren dies in einem Theorem.

Theorem 1.21: Kopplung der Purkinjegruppen mit einer Golgizelle

Jede Purkinjegruppe wird an ihrem Ende von einer Golgizelle abgeschlossen.

Die Startgruppe des Cerebellumclusters endet mit einer Golgizelle,  nach ihr folgt die nächste Purkinjegruppe, die wiederum mit einer Golgizelle endet.  Dies setzt sich bis zum Ende der Kette von Purkinjegruppen fort.

Somit befindet sich zwischen zwei Purkinjegruppen jeweils eine Golgizelle. Nach dieser elementaren Nennung der Fakten müssen wir die systemtheoretische Funktion der Golgizellen herleiten.

Bekanntlich bilden die Golgizellen Komplexsynapsen, in die einerseits die Moosfasern und andererseits die Körnerzellen involviert sind. Hierbei wird davon ausgegangen, dass die Golgizellen generell eine hemmende Wirkung haben, da sie den Transmitter GABA benutzen. In der Literatur findet man am häufigsten die Annahme, die Golgizelle würde die Weiterleitung des Moosfaserinputs zu den Körnerzellen hemmen. Hierbei schiebt sich das Axon der Golgizelle zwischen das Axon der Moosfaser und den Dendriten der Körnerzelle. Dadurch entsteht eine Komplexsynapse mit drei beteiligten Partnern.

Andererseits findet man in der Fachliteratur auch Darstellungen, bei denen die Golgizellen hemmende Synapsen sowohl mit den Moosfasern als auch hemmende Synapsen mit den Körnerzellen bilden, diese aber räumlich voneinander getrennt sind.

Der Autor entschließt sich aus systemtheoretischen Gründen, letztere Variante zu bevorzugen. In diesem Falle hemmt die Golgizelle einerseits die Weiterleitung der Erregung entlang der Moosfaser, die von der hemmenden Synapse an signallos wird. Andererseits hemmt die Golgizelle ebenfalls die erreichbaren aufsteigenden Axone der Körnerzellen, so dass diese noch vor dem Erreichen ihrer Verzweigung in die sogenannten Parallelfasern signallos werden. So wird quasi eine doppelte Weiterleitungshemmung bewirkt: die Signalweiter-leitung wird sowohl auf den Moosfasernaxonen als auch auf den Körnerzellaxonen unterdrückt.

Hier sei an die Literaturquelle 42 erinnert, die im Verzeichnis der benutzten Hilfsmittel aufgelistet ist. In einem hervorragenden Internet-Script von Prof. John K. Harting von der University of Wisconsin Medical School unter dem Titel „The Global Cerebellum ´97“ findet man die von David P. Van Lieshout illustrierte Darstellung der Kopplung von Moosfasern, Körnerzellen und Golgizellen dargestellt. Diese hervorragende Abbildung möge hier als Bildzitat verwendet werden, was in wissenschaftlichen Arbeiten durchaus erlaubt ist. Deutlich ist in dieser Abbildung zu sehen, dass es nicht unbedingt „Komplexsynapsen“ sein müssen. Der hemmende synaptische kontakt der Golgizelle zur Moosfaser kann auch räumlich getrennt vom erregenden synaptischen kontakt der Moosfaser zur Körnerzelle angeordnet sein. In diesem Falle wäre die Weiterleitung der Moosfasersignale entlang der Moosfaser immer dann unterbrochen, wenn die Golgizelle die Moosfaser hemmt.

Skizze 1.23: Bildzitat: Golgizellen hemmen Moosfasern - Quelle siehe (41):

                                                                                             

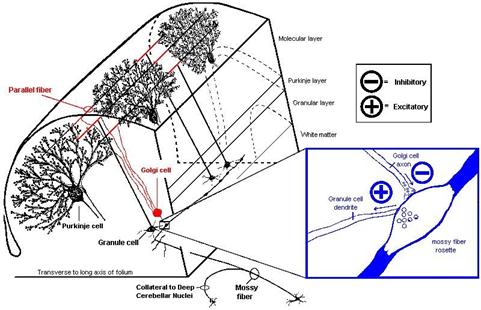
(Ende des Bildzitats)

Wir fassen dies in ein neues Theorem.

Theorem 1.22: Doppelte Weiterleitungshemmung durch die Golgi-Zellen

Jede Purkinjegruppe wird an ihrem Ende mit einer Golgizelle beendet. Diese Golgizelle verursacht eine doppelte Weiterleitungshemmung im Cerebellumcluster.

Einerseits hemmt diese Golgizelle im Aktivitätsfall alle aktiven Moosfasersignale an der Weiterleitung entlang dieser Moosfasern zu den benachbarten Purkinjegruppen, so dass diese keinerlei Parallelfaserinput über Körnerzellen erhalten können, welche die betreffenden Moosfasern hinter der Golgizelle anzapfen.

Andererseits hemmt diese Golgizelle einen Großteil der sich in ihrer unmittelbaren Nähe befindlichen Körnerzellen, so dass deren Parallelfaseraxone signallos werden.

Natürlich taucht die Frage auf, welchem Zweck diese doppelte Weiterleitungshemmung dient. Es wird sich zeigen, dass dadurch eine Mehrfachprägung verschiedener, benachbarter Purkinjegruppen mit dem gleichen Prägungssignal effektiv verhindert werden kann. Die benachbarte Purkinjegruppe kann nicht mit dem gleichen Signal geprägt werden, da dieses sie wegen der doppelten Fortleitungshemmung nicht mehr erreicht. Voraussetzung ist jedoch, dass die zugehörige Golgizelle zur richtigen Zeit aktiviert wird, damit die doppelte Weiterleitungshemmung eintritt.

Dies ist nötig, wenn eine ungeprägte Purkinjezelle mittels Kletterfasersignal geprägt werden soll. In diesem Falle verhindert die doppelte Weiterleitungshemmung, dass die Nachbar-Purkinjegruppen das Moosfasersignal erhalten. Somit wird es unmöglich, viele benachbarte Purkinjegruppen mit dem gleichen Signal in „einem Ritt“ zu prägen. Wie wird dies im Cerebellum realisiert?

Das Argument, eine geprägte Purkinjezelle verhindere die Prägung weiterer Zellen mit dem gleichen Signal dadurch, dass ihr zugehöriges Outputneuron im Kleinhirnkern das Kletterfasersignal in der Olive wirksam unterdrückt, zählt hier nicht. Denn die Frage bezieht sich auch auf einen Zeitpunkt, als das aktuelle Prägungssignal noch gar keine Purkinjezelle okkupiert (also geprägt) hat.

 

Hier erinnern wir uns an das Zitat aus der „Anatomie“ von Graumann/Sasse auf Seite 280, welches hier nochmals wiedergegeben sein möge:

 

„Kletterfasern kontaktieren Dendriten von Golgi-Zellen. Diese hemmen die Körnerzellen und unterbrechen so die Weiterleitung des Moosfaserinputs.“

 

Erhält also eine Purkinjegruppe das stark erregende Kletterfasersignal zugeführt, so werden mit diesem Kletterfasersignal nicht nur die Purkinjezellen der Gruppe erregt, sondern auch die am Gruppenende vorhandene Golgizelle. Diese unterbricht dadurch die Weiterleitung des Moosfaserinputs zu den übrigen benachbarten Purkinjegruppen des Cerebellumclusters.

Ohne Moosfaserinput erhalten aber die Parallelfasern keine Signale, so dass eine Prägung durch ein Kletterfasersignal nicht mehr möglich ist. Denn sowohl eine Langzeitdepression als auch eine Langzeitpotenzierung benötigen neben dem tetanischen (höherfrequenten) Input über das Kletterfaseraxon zusätzlich den Input über die Parallelfasern. Dies gilt sowohl für die Langzeitdepression der Synapsen zwischen Parallelfasern und Purkinjezellen als auch für die Synapsen zwischen Parallelfasern und Sternzellen bzw. Korbzellen. Daher eignen sich die Golgizellen speziell wegen ihres dendritischen kontaktes zu den Kletterfasern hervorragend dazu, während des Prägungsvorganges die Inputzufuhr über die Moosfasern abzuwürgen und so die Prägung benachbarter Purkinjegruppen zu verhindern.

 

Wenn wir uns also die Purkinjegruppen entlang der Parallelfasern angeordnet denken und davon ausgehen, dass (zunächst) zwischen je zwei Purkinjegruppen auch eine Golgizelle liegen möge, wird verständlich, warum ein Kletterfasersignal nur die erste freie Purkinjegruppe der Reihe prägen kann. Die auf die erste freie Purkinjegruppe folgende Golgizelle unterbricht den Signalfluss zwischen Moosfasern und Körnerzellen auf Grund der starken Erregung, die ihr wegen des Kletterfaserkontaktes zuteilwird. Daher können die übrigen Purkinjegruppen, Sternzellen und Korbzellen, die auf die erste (freie) Purkinjegruppe folgen, keinerlei Erregung über die Parallelfasern erhalten. Dies gilt sogar, bevor die erste freie Purkinjegruppe durch dieses Kletterfasersignal geprägt worden ist. Für die Entstehung von Langzeitpotenzierung (LTP) sowie Langzeitdepression (LTD) ist aber nicht nur die tetanische Erregung durch das eintreffende Kletterfasersignal vonnöten, sondern ebenso wichtig ist die Erregung der Zellen über die Parallelfasersignale. Diese werden aber von der ersten Golgizelle, die auf die erste freie Purkinjezelle folgt, völlig „abgewürgt“. Daher kann ein eintreffendes Kletterfasersignal immer nur die erste freie Purkinjegruppe prägen, während die restlichen (fast) gar keinen Parallelfaserinput mehr erhalten. Deshalb haben die Golgi-Zellen im Cerebellum eine wichtige Funktion. Jedoch ist diese Aufgabe nicht ihre einzige, wie später gezeigt werden wird. Ebenso wird noch geklärt werden müssen, warum die Kletterfasern neben den Purkinjezellen und Golgizellen ebenfalls die Korbzellen und Sternzellen kontaktieren.

 

Die obigen Ausführungen gelten (zunächst) unter der einschränkenden Bedingung, dass die Länge der Parallelfasern und die räumliche Ausdehnung einer Purkinjegruppe in Richtung der Parallelfasern sich nicht wesentlich voneinander unterscheiden und dass die Körnerzellen, aus deren Axonen letztlich die Parallelfasern entstehen, sich vorwiegend am Anfang einer Purkinjegruppe befinden. Vorausgesetzt wird auch eine Signaldämpfung bei der Ausbreitung der Signale entlang der Parallelfasern, ebenso möge die Ausbreitungsgeschwindigkeit der Aktionspotentiale entlang der Parallelfasern deutlich geringer sein als entlang der Moosfasern. Später werden wir erkennen, dass eine zunehmende Länge der Parallelfasern über die Grenze einer Purkinjegruppe hinweg zu den Nachbargruppen zusätzliche Prägungsmöglichkeiten bringt. (Siehe Teil 2.13.  „Der cerebellare Nachhall“ in dieser Monografie)

Die Aufgabe der im Cerebellum vorhandene Sternzellen und Körnerzellen wird in den nachfolgenden Ausführungen erklärt werden. Doch vorher müssen wir uns dem Phänomen der Prägung der Purkinjezellen widmen. Die Prägung der Purkinjezellen wird nach der Theorie des Autors vorwiegend durch die Langzeitdepression und Langzeitpotenzierung bewirkt wird. Dieses wurde bereits vor langer Zeit vermutet. Diese Monografie wird versuchen, den exakten Nachweis dafür zu erbringen.

 

Bei RAM-Speichern von Computern wird der Inhalt einer RAM-Zelle durch einen Schreibbefehl gespeichert. Erhält eine solche Speicherzelle einen Schreibbefehl, so speichert sie genau die Daten, die in diesem Moment auf den Datenleitungen liegen, dauerhaft als Binärwerte ab. Die abgespeicherten Daten können später mit einem Lesebefehl wieder ausgelesen werden. Sie gehen erst verloren, wenn die Stromzufuhr des Computers abgeschaltet wird.

Der Autor behauptet, die Abspeicherung der Daten bei Purkinjezellen erfolge analog über einen Schreibbefehl. Er unterstellt sogar, der Schreibbefehl wäre das Kletterfasersignal, über das bisher viele Vermutungen geäußert wurden.

Sollte dies zutreffen, gäbe es neben dem neuronalen Systemtakt eine weitere Gemeinsamkeit zwischen Computer und Gehirn: den Schreibbefehl zum Abspeichern.

Die Purkinjezellen wären dann als neuronaler RAM-Speicher einzustufen.

Das Werk „Das Gehirn“ von Richard F. Thompson vom Spektrum Akademischer Verlag war das erste neurologische Fachbuch des Autors, das dieser aus Anlass seines Geburtstages von seinen Arbeitskolleginnen geschenkt bekam – in Form eines Gutscheines.

In diesem ausgezeichnetem Buch beschreibt F. Thompson auf Seite 104 die Entdeckung der Langzeitpotenzierung. Dem Leser wird ein wörtliches Zitat daraus angeboten:

 (Zitatanfang – Seite 104)

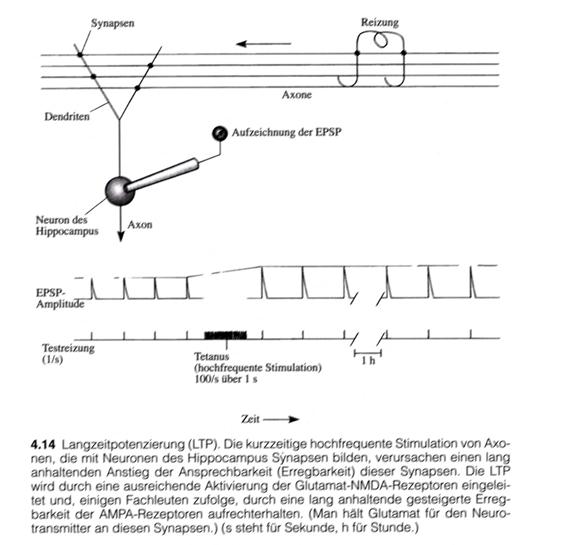
„Als der norwegische Wissenschaftler T. Lømo und sein britischer Kollege Tim Bliss 1970 in Per Andersons Labor in Oslo untersuchten, wie der Hippocampus auf elektrische Reizung seiner zuführenden Leitungsbahnen synaptisch reagiert, machten sie eine Entdeckung: Wenn sie eine zuführende Leitungsbahn kurzzeitig mit hoher Frequenz (beispielsweise eine Sekunde lang mit 100 Hertz, das heißt mit 100 Reizen pro Sekunde) stimulierten, nahm die synaptische Antwort des Hippocampus auf einzelne Teststromstöße an derselben Bahn dramatisch zu, und diese Reaktionsstärke blieb über den gesamten Testzeitraum erhalten (Abbildung 4.14). Die Untersucher nannten dieses Phänomen Langzeitpotenzierung (LTP).“

„Das Bemerkenswerte an dieser Potenzierung war, dass sie nach solch einer kurz dauernden Reizung so lange anhielt.“

(Zitatende)

Es sei gestattet, auch die genannte Abbildung hier als „Bildzitat“ zu verwenden, damit der Vorgang der Langzeitpotenzierung bildlich verdeutlicht wird.

Skizze 1.24: LPT und LTP im Hippocampus - (Bildzitat – Seite 105 – Abbildung 4.14)

 

(Ende des Bildzitates zur Langzeitpotenzierung)

In der Zeichnung wird eine Zelle des Hippocampus dargestellt, die über Axone erregt werden kann. Die Erregung überträgt sich von den Axonen über die Synapsen zu den Dendriten des Hippocampusneurons und führt dort zum Anstieg der Membranspannung. Letztere wird elektronisch gemessen.

Reizt man die zuführenden Axone durch externe Zuführung geeigneter elektrischer Signale, wie in der Abbildung dargestellt, so kann die Änderung des Membranpotentials aufgezeichnet werden.

Eine kurzzeitige, hochfrequente Erregung – in der Neurologie als tetanische Erregung bezeichnet – führt hier beim Hippocampusneuron zur Entstehung der Langzeitpotenzierung. Durch die Langzeitpotenzierung wird die Erregbarkeit längerfristig deutlich gesteigert. Dieser Effekt hält über lange Zeit an. LTP und LTD werden seit längerem als Mechanismen für die Entstehung von Langzeitgedächtnis angesehen. Bisher fehlte lediglich eine konkrete neuronale Schaltung, die sich im realen Gehirn nachweisen ließ. Diese versucht der Autor hier vorzulegen.

Quelle der Zitate: „Das Gehirn“ von Richard F. Thompson vom Spektrum Akademischer Verlag, 2001

Die Langzeitpotenzierung (LTP, long-term potentation) ist nur eine Variante, eine zweite ist die Langzeitdepression (LTD, long-term depression). Bei dieser zweiten Variante bewirkt die gleiche Ursache – eine tetanische (höherfrequente) Reizung und gleichzeitige präsynaptische Erregung eine starke und dauerhafte Verminderung der synaptischen Kopplung.

Nach diesem Text- und Bildzitat tragen wir vorsorglich alle noch nicht genannten, aber inzwischen weltweit bekannten Fakten zur Cytoarchitektur des Cerebellums zusammen, um den Prägungsalgorithmus für die Purkinjezellen zu erklären.

Zunächst soll auf einige Besonderheiten der Kletterfaserprojektion eingegangen werden, die später das Verständnis der Funktionsweise der Prägung der Purkinjezellen erleichtern werden. Im Band 4 der „Anatomie“ von Graumann/Sasse mit dem Titel „Sinnessysteme-Haut-ZNS-Periphere Leitungsbahnen“ vom Schattauer-Verlag lesen wir auf Seite 208:

(Zitatbeginn:)

„Die Kletterfasererregung wird insgesamt über die gleichen Mechanismen moduliert wie die Moosfasererregung:

·         Kletterfasern kontaktieren mit ihren Axonkollateralen die Sternzellen, diese hemmen die Purkinje-Zellen im Sinne einer Vorwärtshemmung.

·         Kletterfasern aktivieren über Axonkollaterale Korbzellen, die parallel geschaltete Purkinje-Zellen inhibieren und so eine Laterale Hemmung bewirken.

·         Kletterfasern kontaktieren Dendriten von Golgi-Zellen. Diese hemmen die Körnerzellen und unterbrechen so die Weiterleitung des Moosfaserinputs. Dies ist der einzige Ort in der Kleinhirnrinde, an der eine Einflussnahme des Kletterfasersystems auf das Moosfasersystem möglich ist. Die Hemmung, die hier erfolgt, wird als heterosynaptische Inhibition bezeichnet, da sie zwischen zwei unterschiedlichen Systemen auftritt.“

(Zitatende)

Zu den Korbzellen hier sei ebenfalls aus dem Lehrbuch „Anatomie Band 4“ von Graumann/Sasse zitiert. Auf Seite 279 heißt es:

(Zitatbeginn:)

„Korbzellen sind mittelgroße hemmende Interneurone. Sie liegen im Stratum moleculare, in der Nähe der Perykaryen der PURKINJE-Zellen. Ihr Dendritenbaum erstreckt sich in das Stratum moleculare, ihr Axon umspinnt mit zahlreichen feinen Verzweigungen korbartig Perykaryon und Axonhügel von acht bis zehn benachbarten PURKINJE-Zellen. Korbzellen sind für die laterale Hemmung von PURKINJE-Zellen verantwortlich.“

 

                                                                                  (Zitatende)

 

An dieser Stelle sei den Herausgebern, Herrn Prof. Walter Graumann aus Tübingen und Herrn Prof. Dieter Sasse aus Basel sowie allen beteiligten Mitautoren gedankt für dieses überaus gelungene Fachbuch. Seine besondere Qualität besteht in der Anschaulichkeit der Darlegungen, so dass letztendlich sogar ein Mathematiker detaillierte Vorstellungen über die innere Architektur der neurologischen Subsysteme entwickeln konnte.

Wenn die Korbzellen mittelgroße Interneurone sind, die in der Nähe der Zellkörper der Purkinjezellen liegen, so könnte man folgern, dass jede Purkinjezelle ihre eigene Korbzelle hat. Sonst gäbe es recht viele Purkinjezellen, in deren Nähe keine Korbzellen vorhanden wären. Eine solche unregelmäßige Verteilung wäre in der Literatur sicherlich erwähnt worden. Daher postulieren wir, dass eine jede Purkinjezelle eine eigene Korbzelle besitzt. Wir werden diese Korbzelle als spezifische Korbzelle der Purkinjezelle bezeichnen. Sollten in der Nähe jeweils mehrere Korbzellen zu einer Purkinjezelle gehören und mit ihr zusammenwirken, so werden wir sie gedanklich zu einer einzigen, abstrakten Korbzelle zusammenfassen, so dass diese eine (gedachte) Korbzelle ersatzweise die gewünschte Arbeit leistet.

 

Definition 1.23: Spezifische Korbzelle einer Purkinjegruppe

Eine Korbzelle, deren Zellkörper sich in der Nähe einer Purkinjezelle befindet, so dass sowohl die Purkinjezelle als auch die Korbzelle eine gewisse Auswahl von Parallelfasern gemeinsam kontaktieren, bezeichnen wir als spezifische Korbzelle der Purkinjegruppe.

Theorem 1.23: Korbzellentheorem

In jeder Purkinjegruppe verfügt jede Purkinjezelle über eine spezifische Korbzelle in ihrer unmittelbaren Nähe. Diese Korbzelle erhält erregenden Input von den erreichbaren Parallelfasern und erhält ebenfalls erregenden Kletterfaserinput. Diese Korbzelle selbst hemmt im Erregungsfalle alle Purkinjezellen der Purkinjegruppe, der sie angehört.

Das Theorem unterstellt nicht, dass eine Korbzelle keine hemmende Wirkung auf Purkinjezellen von benachbarten Purkinjegruppen haben kann. Für die Lernfähigkeit ist jedoch die Hemmung aller Purkinjezellen der gleichen Gruppe wesentlich wichtiger und wird deshalb besonders gewürdigt. Es wird sich später zeigen, dass jede Korbzelle alle Purkinjezellen in einem gewissen Raumgebiet hemmt, so dass eine Art rezeptives Hemmungsfeld entsteht. Hier wäre der Nachweis vonnöten, dass sich das Axon radial in alle Richtungen verzweigt und jedes Teilaxon beispielsweise acht bis zehn Purkinjezellen hemmt. Schneidet man die Cerebellumschicht entlang einer Ebene auf, so sieht man nur noch die Axonverzweigung parallel zur Schnittebene, während die übrigen Verzweigungen nicht oberflächennah verlaufen und dadurch vom restlichen Material verdeckt werden. Dies also gilt es noch zu prüfen.

Für den Nachweis, dass das Cerebellum einen Speicher für Komplexsignale darstellt, der sequentiell organisiert ist, benötigen wir noch einige inzwischen gut bekannte Fakten über die Wirkung der Purkinjezellen auf die Interneuronen des Cerebellums.

Zu den Purkinjezellen hier sei ebenfalls aus dem Lehrbuch „Anatomie Band 4“ von Graumann/Sasse zitiert. Auf Seite 281 heißt es:

 

(Zitatbeginn:)

 

„Eine zusätzliche Modulation erfolgt über die efferenten Neurone der Kleinhirnrinde, die Purkinje-Zellen. Diese senden Axonkollateralen zu allen Interneuronen der Kleinhirnrinde. Die resultierende Hemmung von hemmenden Neuronen führt zu einer Aufhebung der Hemmung, zur Disinhibition.“

 

                                                                                  (Zitatende)

Aus obigem Zitat ist eine wesentliche Folgerung für die Golgizellen ableitbar, die für die systemtheoretische Funktionsweise des Cerebellums äußerst bedeutsam ist:

Die Golgizellen werden von Axonkollateralen der Purkinjezellen gehemmt.

Dieser Fakt ist für die Steuerung der Weiterleitungshemmung entlang der Moosfasern äußerst wichtig, speziell im Falle der Nichterkennung und der Erkennung eines Signals durch eine Purkinjezelle. Die Weiterleitungshemmung im Falle der Signalerkennung hat ein funktionelles Gegenstück: die Unterdrückung der Weiterleitungshemmung im Falle der Nichterkennung. Da eine nichterkennende Purkinjezelle stark erregt ist, hemmt sie mit ihrer Erregung die Golgizelle, so dass diese inaktiv ist. Dadurch können die Moosfasersignale von der Golgizelle nicht an ihrer weiteren Ausbreitung entlang der Moosfasern zu den Nachbargruppen gehindert werden. Die Weiterleitungshemmung kann also durch ein aktives Kletterfasersignal angeschaltet und durch die aktive Purkinjezelle abgeschaltet werden.

Dass auch Korbzellen und Sternzellen von den Kollateralaxonen der Purkinjezellen gehemmt werden können, wird sich später als sinnvoll erweisen.

Da nach Ansicht des Autors die kleinste Organisationseinheit des Cerebellums die Purkinjegruppe ist, die an ihrem Ende von je einer Golgizelle abgeschlossen ist, ordnen wir die hemmenden Axonkollateralen der Purkinjegruppen genau dieser einen Golgizelle zu. Somit wird nach Ansicht des Autors jede Golgizelle von den Purkinjezellen der Purkinjegruppe gehemmt, zu der sie gehört. Der Sinn dieser hemmenden Verbindung wird sich noch zeigen. Wir fassen jedoch diesen Zusammenhang in ein eigenes Theorem.

Theorem 1.24: Hemmung der Golgizelle durch die Purkinjezellen der zugehörigen Purkinjegruppe

Die Golgizelle einer Purkinjegruppe wird von den Purkinjezellen dieser Gruppe gehemmt, wenn diese Purkinjezellen aktiv sind.

Am Ende der theoretischen Darstellungen zum Cerebellum werden wir die paradoxe Situation erkennen, dass im Cerebellum quasi jedes Neuron mit jedem Neuron synaptische verbunden ist, und die neuronale Schaltung des Cerebellums dennoch sinnvoll funktioniert.

Als letzte Vorüberlegung zur Grundschaltung des Cerebellums müssen wir hypothetisch klären, wie der Signalfluss von den Moosfasern zu den Purkinjezellen erfolgt.

Offenbar sind die Moosfasern ein sequentielles Verteilungssystem.

Daher denken wir uns ein Cerebellumcluster beispielsweise aus n Purkinjegruppen aufgebaut. Jede Purkinjegruppe möge den gleichen Input erhalten. Daher soll jeder Purkinjegruppe für jede Moosfaser auch genau eine Körnerzelle zugeordnet sein, die diese Moosfaser innerhalb des räumlichen Ausdehnungsgebietes dieser Gruppe anzapft und ein aufsteigendes Axon bildet, welches sich in der Molekularschicht T-förmig in beide Richtungen verzweigt.

Wenn nun die Länge dieser Parallelfasern so groß ist, dass davon k Purkinjegruppen erreicht werden, so haben diese k Purkinjegruppe ihrerseits ebenfalls je genau eine Körnerzelle, die die gleiche Moosfaser anzapft. Daher wird jede dieser Purkinjegruppen insgesamt k Parallelfasern besitzen, die alle von der gleichen Moosfaser abgeleitet sind. Und je mehr Purkinjegruppen es gibt und je länger die Parallelfasern werden, umso mehr Parallelfasern erhalten ihren Input von der gleichen Moosfaser. Insofern ist das Moosfasersystem ein sequentielles Signalverteilungssystem für die Purkinjegruppen.

Theorem 1.25: Das Moosfasersystem als sequentielle Verteilungssystem

Das Moosfasersystem verteilt den Cortexoutput sequentiell auf alle Purkinjegruppen. Jede Purkinjegruppe erhält von jeder Moosfaser den Input über genau eine eigene Körnerzelle. Durch die große Länge der Parallelfasern erhält jedoch jede Purkinjegruppe auch den Input über die Parallelfasern, die in den Nachbargruppen von der gleichen Moosfaser stammen. Dadurch ist die Anzahl der Parallelfasern, deren Input von der gleichen Moosfaser stammt, gleich der Anzahl der Purkinjegruppen, die von ein- und derselben Moosfaser Input erhalten. Die Ausbreitungsgeschwindigkeit der Aktionspotentiale entlang der Moosfasern ist relativ hoch, so dass alle Purkinjegruppen das auszuwertende Signal (fast) gleichzeitig erhalten und (fast) gleichzeitig mit der Signalanalyse beginnen können.

Wenn hier eine Purkinjegruppe jede Moosfaser mit genau einer Körnerzelle anzapft, so kann diese Körnerzelle durchaus einen größeren Dendritenbaum bilden, so dass pro Körnerzelle mehrere (oder viele) synaptische kontakte zur Moosfaser entstehen (rosettenartiges Anzapfen).

Die Parallelfasern zu einer bestimmten Purkinjegruppe lassen sich nunmehr in 2 Gruppen einteilen. Wir tun dies in einer Definition.

Definition 1.24: Primäre und sekundäre Parallelfasern einer Purkinjegruppe

Eine Parallelfaser, deren Körnerzelle innerhalb des von der zugehörigen Purkinjegruppe beanspruchten Gebietes liegt und dort eine Moosfaser kontaktiert, wird primäre Parallelfaser dieser Purkinjegruppe genannt. Eine Parallelfaser, die eine Purkinjegruppe kontaktiert, aber deren Körnerzelle außerhalb des von dieser Gruppe beanspruchten Gebietes liegt, wird sekundäre Parallelfaser genannt.

Damit können wir ein weiteres Theorem aufstellen.

Theorem 1.26: Projektion des Cortex in eine Purkinjegruppe

Jedes Signalneuron eines Cortexclusters projiziert über das Moosfasersystem mit genau einer primären Parallelfaser in jede Purkinjegruppe. Die übrigen Parallelfasern dieses Signalneurons erreichen jede Purkinjegruppe als sekundäre Parallelfasern, deren Ursprung in den Nachbargruppen des gleichen Cerebellumclusters liegt.

Damit wird das Cerebellum durch sequentielle Aneinanderreihung eines Grundelementes gebildet. Diese Grundstruktur ist die Purkinjegruppe, die zugehörige Golgizelle, die primären Parallelfasern, die zur Gruppe gehörenden Körnerzellen, Korb- und Sternzellen, sowie die beiden Kernneuronen, von denen eines erregend, das andere hemmend ist. Des Weiteren gehört zu einer Purkinjegruppe ein Kletterfaseraxon, welches mit Ausnahme der Körnerzellen alle Neuronen der Gruppe kontaktiert. Bei der Startgruppe ist dieses Kletterfaseraxon das primäre, während alle übrigen Gruppen je ein sekundären Kletterfaseraxon zugeordnet ist.

Es gibt die mögliche Variante, dass eine Körnerzelle synaptischen kontakt zu mehreren, verschiedenen Moosfasern haben könnte. Das nachfolgende mathematische Prinzip der Prägung von Purkinjezellen wird durch eine solche Verallgemeinerung nicht hinfällig, sondern kann daran angepasst werden.

In der verfügbaren Literatur gibt es leider keinen Hinweis darauf, warum es im Cerebellum Korbzellen und Sternzellen gibt. Beide Arten von Neuronen werden vom Parallelfaserinput erregt und hemmen beide die Purkinjezellen. Während die Korbzellen sich im unteren Teil der Molekularschicht befinden und die dort befindlichen Parallelfasern synaptisch anzapfen, befinden sich die Sternzellen in der äußeren Region der Molekularschicht und beschränken ihre synaptischen kontakte auf dieses Gebiet. Den Korbzellen wird wegen der direkten Hemmung der Zellkörper der Purkinjezellen oft auch eine stärkere Hemmungswirkung zugesprochen. Den Sternzellen traut man eher eine modulatorische Wirkung zu.

Daher vermutet der Autor eine gewisse Aufgabenteilung zwischen Sternzellen und Korbzellen. Diese soll im nachfolgenden Theorem ausgesprochen werden.

Theorem 1.27: Arbeitsteilung Korbzellen und Sternzellen

Die Signalneuronen eines Cortexclusters projizieren über eine primäre Moosfaserpopulation ins Cerebellum. Die aus dieser Moosfaserpopulation über die Körnerzellen abgeleitete Parallelfaserpopulation wird ausschließlich von den Korbzellen synaptisch kontaktiert.

Eine weitere Moosfaserpopulation entstammt dem aufmerksamkeitssteuernden System (ARAS *) des Gehirns. Dazu zählt der Autor unter anderem die Formatio reticularis sowie die magnocellularen Mittelwertsignale der Cortexschicht V, die letztlich über den Nucleus centromedianus zum Cortex zurückfinden (siehe Auflösungspyramide) und von dort über die Brückenkerne zu den Moosfasern des Cerebellums gelangen. Die daraus abgeleiteten Parallelfasern werden ausschließlich von den Sternzellen kontaktiert.

* ARAS: Aufsteigendes retikuläres Aktivierungssystem

Die Parallelfasern, die ausschließlich von den Korbzellen kontaktiert wird, werden wir als direkte cortikale Parallelfasern bezeichnen. Die Parallelfasern, die ausschließlich die Sternzellen kontaktieren, nennen wir indirekte Parallelfasern. Ebenso unterscheiden wir direkte und indirekte Moosfasern, je nachdem, ob sie die direkten oder indirekten Parallelfasern speisen. Daher gilt die nachfolgende Definition.

Definition 1.25: Direkte und indirekte Moosfasern/Parallelfasern

Die Moosfasern, die den cortikalen Input aus dem Cortexcluster zu denjenigen Parallelfasern transportieren, die die Korbzellen und die Purkinjezellen erregen, nennen wir die direkten Moosfasern. Das zugehörige Signal bezeichnen wir als direktes Cortexsignal. Die Parallelfasern, die ihren Input von den direkten Moosfasern erhalten, nennen wir direkte Parallelfasern.

Die übrigen Moosfasern bezeichnen wir als indirekte Moosfasern. Sie kontaktieren ausschließlich die Sternzellen sowie die Purkinjezellen. Das zugehörige Signal werden wir als das indirekte Signal und die Parallelfasern als die indirekten Parallelfasern bezeichnen.

Damit speisen die Signalneuronen des Cortex die direkten Moosfasern und die direkten Parallelfasern mit den direkten Cortexsignal. Das direkte Cortexsignal endet an den Korbzellen und den Purkinjezellen des Cerebellums.

Die restlichen Neuronen, die ins Cerebellum projizieren, speisen die indirekten Moosfasern und die indirekten Parallelfasern mit dem indirekten Cortexsignal, welches an den Sternzellen und den Purkinjezellen des Cerebellums endet.

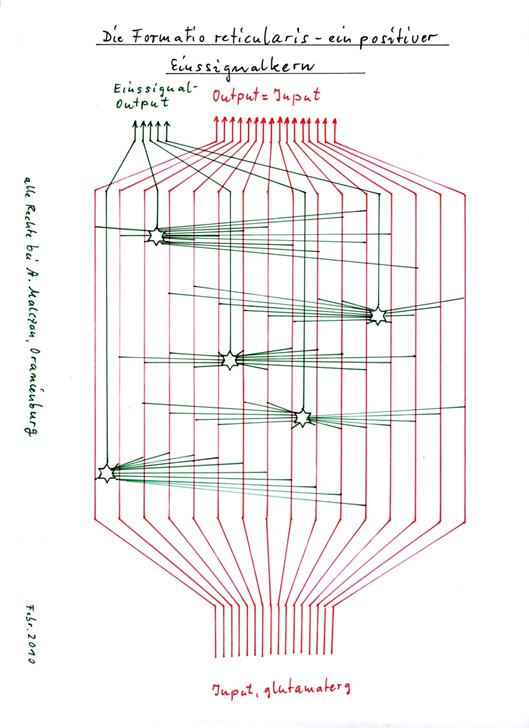
Die Sinnhaftigkeit dieser Zweiteilung in der Herkunft der Moos- und Parallelfasern wird sich noch zeigen. Die Parallelfasern der Sternzellenpopulation jedenfalls befinden sich in der Molekularschicht weiter außen und sind daher vermutlich evolutionär älter. Sie gehören dem magnocellularem System an, zu dem auch die Formatio reticularis gehört. Nach Ansicht des Autors ist die aufsteigende Formatio reticularis ein Einssignalkern. Als Besonderheit kommt hinzu, dass es in der aufsteigenden Formatio reticularis mehrere solcher einssignalbildenden Kerne gibt, die zudem unterschiedliche Transmitter verwenden. Das typische Kennzeichen solcher Einssignalkerne sind die magnocellularen Einssignalneuronen mit ihren riesigen Dendritenbäumen. In der „Funktionellen Neuroanatomie“ von Zilles /Rehkämper, 3. Auflage, Seite 318/319 lesen wir dazu:

 

(Zitatbeginn:)

 

„Die Formatio reticularis erstreckt sich vom Mesencephalon bis ins kaudale Ende der Medulla ablongata. Die medialen zwei Drittel bestehen aus großen, das laterale Drittel aus kleinen Neuronen.“ ... „Die großen Neurone der magnocellularen Zone haben weit ausstrahlende Dendriten, die sich in einer Ebene senkrecht zur Längsachse des Rhombencephalons verzweigen. Dabei überlappen die dendritischen Territorien der verschiedenen Neurone stark. Daher kann ein einzelnes, großes Neuron Informationen aus einem großen Einzugsgebiet in der transversalen Ebene und gleichzeitig aus vielen Fasersystemen, die senkrecht zu dieser Ebene durch den Hirnstamm ziehen, aufnehmen. Dies ist die strukturelle Grundlage der integrativen Funktion der Formatio reticularis.“

 

                                                                                                                      (Zitatende)

 

Angesichts der großen Bedeutung der Formatio reticularis im aufsteigenden Aktivierungssystem und für das indirekte Signal im Cerebellum fassen wir unsere Erkenntnisse in eigenes Theorem, welches wir mit den Namen der Inspirationsgeber versehen.

Theorem 1.28 von Zilles/Rehkämper: Einssignalneuronen in der Formatio reticularis

Die erregenden großen Neurone der magnocellularen Zone der Formatio reticularis bilden als Integrationsneurone positive Einssignale, deren Signalstärke S mit zunehmender Stärke des integrierten Inputs wächst. Hierbei sind verschiedene Transmitter verschiedenen Signalmodalitäten zugeordnet.

Skizze: 1.25: Die Formatio reticularis – ein positiver Einssignalkern

Erstmalig wird die Existenz von Einssignalneuronen in der Formatio reticularis in der 25-seitigen Monografie „Die neuronale Schaltung des Gehirns – Teil 1: Negationskerne“ vom 07.03.2010 erwähnt, die ebenfalls aus der Feder des Autors dieser Monografie stammt und an den Verlag „Gehirn und Geist“, genauer an Herrn Hartwig Hanser auf dessen Anforderung am 07.März 2010 um 15.28 Uhr per E-Mail zugeschickt wurde. Am 20. April 2010 erhielt der Autor die Mitteilung von Herrn Hanser, dass der Verlag eine Veröffentlichung nicht in Erwägung ziehen würde. Daraus zog der Autor den Schluss, dass die Qualität der Arbeit noch nicht den nötigen Stand erreicht hatte. Tatsächlich zeigte sich fast ein Jahr später, dass einige neuronale Kerne, die in dieser Schrift als Einssignalkerne beschrieben wurden, diese Eigenschaft wirklich nicht hatten. Die Euphorie, reale Einssignalkerne entdeckt zu haben, hatte dazu geführt, zu viele Neuronenkerne zu dieser Kernklasse gezählt zu haben. Die Kriterien waren scheinbar erfüllt, aber diese Annahmen erwiesen sich später als Irrtum. Andere neuronale Kerne wurden erst viel später als Einssignalkerne, Negationskerne oder Inversionskerne erkannt.

Während der synaptische kontakt zwischen Kletterfasern und Korbzellen im Allgemeinen anerkannt wird, ist der Nachweis eines synaptischen kontaktes zwischen Kletterfasern und Sternzellen weniger vorstellbar. Die Sternzellen liegen locker verteilt zwischen den Purkinjezellen. Dennoch folgen wir den Ausführungen von Graumann/Sasse in der „Anatomie“ auf Seite 280:

(Zitatbeginn)

„Kletterfasern kontaktieren mit ihren Axonkollateralen die Sternzellen, diese hemmen die Purkinje-Zellen im Sinne einer Vorwärtshemmung.“

                                                                                              (Zitatende)

Nachdem wir also erkannt haben, dass die Kletterfasern sowohl Korbzellen, Sternzellen, Golgizellen und Purkinjezellen sowie die positiven und negativen Kernneuronen kontaktieren, leiten wir daraus den einzig möglichen Schluss ab: Alle diese Zellarten werden nur deshalb von den Kletterfasern kontaktiert, damit die Langzeitdepression bzw. die Langzeitpotenzierung durch die Kletterfasersignale bewirkt werden kann. Eine theoretische Systemanalyse bringt ein noch genaueres Ergebnis, welches wir in ein neues Theorem fassen.

Theorem 1.30: Die Wirkung des Kletterfasersignals auf die Cerebellum-Neuronen

Das Kletterfasersignal bewirkt bei den Purkinjezellen eine Langzeitdepression.

Bei den Korbzellen, den Sternzellen, den Golgizellen sowie den positiven und negativen Kernneuronen bewirkt das Kletterfasersignal eine Langzeitpotenzierung.

Es wäre eine Verschwendung von Material und Arbeit, wenn die Kletterfasern Zellen kontaktieren, um sie ohne weitere Wirkung nur übermäßig zu erregen. Dennoch sollte nicht vergessen werden, dass die Natur nicht zur Sinnhaftigkeit neigen muss. Dies beweist die enorme Vielfalt der knöchernen Auswüchse gerade in der Zeit der Dinosaurier. Diese waren durchaus nicht immer sinnvoll. Aber bei einem gewissen evolutionären Druck erweisen sich „sparsam“ agierende Systeme als vorteilhaft. Daher wären die Kletterfaserkontakte zu allen Cerebellumneuronen wahrscheinlich bereits verkümmert, wenn sie keine „höhere“ Bedeutung hätten. Denn Zeit genug ist ja vergangen, deutlich mehr, als seinerzeit für die Dinosaurier zur Verfügung gestanden hatte. Offenbar sind die Kletterfaserkontakte zu allen Cerebellumneuronen systemtheoretisch notwendig.

Im Hinblick auf die indirekten Moosfasersignale muss erwähnt werden, dass es drei Subtypen des Cerebellums gibt: das Vestibulocerebellum, das Spinocerebellum und das Pontocerebellum. Hier unterschieden sich diese drei Subsysteme durch die Herkunft der indirekten Moosfasersignale. Das Vestibulocerebellum erhält seine indirekten Moosfasersignale (nach der unbestätigten Ansicht des Autors) von der Formatio reticularis. Dies trifft für das Spinocerebellum ebenfalls zu. Aber das Pontocerebellum erhält (evtl. zusätzlich) die indirekten Moosfasersignale von den Mittelwertneuronen der Schicht V, die offenbar nicht nur zum Nucleus subthalamicus ziehen, sondern (wahrscheinlich) auch zu den Brückenkernen. Die indirekte Moosfaserpopulation endet (nach Ansicht des Autors) vorwiegend im Sternzellensystem des Cerebellums und hat dort eine sehr wichtige Aufgabe bei der Steuerung des Arbeitspunktes der Assoziativmatrizen des Cerebellums. Dazu jedoch später.

Wir fassen die bisherigen Vorstellungen in einer Übersicht zusammen.

Theorem 1.31: Grundschaltung des Cerebellums

Das Cerebellum besteht aus Cerebellumclustern. Jedem Cerebellumcluster entspricht ein Cortexcluster. Die Signalneuronen des Cortexclusters projizieren über die Brückenkerne zu den direkten Moosfasern des zugehörigen Cerebellumclusters sowie zu den positiven und negativen Kernneuronen des gleichen Clusters. Dieses Signal stellt das direkte Cortexsignal dar, die projizierenden Moosfasern kontaktieren ausschließlich Körnerzellen, die nur mit den Korbzellen sowie mit den Purkinjezellen und den Golgizellen des Cerebellums Synapsen bilden.

Die indirekten Moosfasern entstammen dem aufmerksamkeitssteuernden System (ARAS) des Gehirns – vermutlich der Formatio reticularis – beziehungsweise dem magnocellularen Mittelwertsystem. Seine Signale erreichen die indirekten Moosfasern, die die indirekten Körnerzellen mit Input versorgen. Deren Axone bilden ein indirektes Parallelfasersystem, welches die Sternzellen, aber auch die Purkinjezellen erregt, jedoch nicht die Korbzellen. Ob dieses indirekte Signal die Golgizellen erreicht, ist unklar, aber eher unwahrscheinlich.

Das Signal des Aktivitätsneurons des Cortexclusters erreicht über das Striosomensystem der Basalganglien das Cerebellumcluster als primäres magnocellulares Kletterfasersignal. Das zugehörige primäre Kletterfaseraxon kontaktiert ausschließlich die Neuronen der ersten Purkinjegruppe, die als Startgruppe fungiert. Alle Purkinjezellen, aber auch jede Korb- und Sternzelle sowie die zugehörige Golgizelle in dieser Startgruppe werden vom primären Kletterfaseraxon kontaktiert, ebenso das positive und das negative Kernneuron dieser Startgruppe.

Das Cerebellumcluster besteht aus einer wohlgeordneten Reihe von Purkinjegruppen mit einer Startgruppe und einer Endgruppe. Jede Purkinjegruppe mit Ausnahme der Endgruppe hat eine Nachfolgergruppe, jede Purkinjegruppe mit Ausnahme der Startgruppe hat eine Vorgängergruppe. Die Reihenfolge der Purkinjegruppen ergibt sich durch ihre räumliche Anordnung entlang der Moosfasern, die ein sequentielles schnelles Verteilungssystem für den Cortexoutput bilden.

Jede Purkinjegruppe endet mit einer Golgizelle, die im Erregungsfalle die doppelte Weiterleitungshemmung bewirkt. Sie unterbricht dann einerseits die Ausbreitung der Moosfasererregung entlang der Moosfasern zu den nachfolgenden Purkinjegruppen. Andererseits unterbricht sie die Weiterleitung der Erregung der von ihr erreichbaren Körnerzellen zu ihren Parallelfasern.

Alle Purkinjezellen, die zugehörige Golgizelle und alle Korbzellen und Sternzellen der übrigen Purkinjegruppen des Cerebellumclusters werden von je einem zugehörigen sekundären Kletterfasersignal erregt, wenn dieses aktiv ist.

Die sekundären Kletterfasersignale werden vom primären Kletterfaserneuron der Olive abgeleitet entweder durch zentrale oder sequentielle Verteilung in der Olive.

Die positiven und negativen Kernneuronen erhalten im Falle einer hinreichenden Aktivität des zugehörigen Cortexclusters ihre Einssignalerregung von den allen Moosfasern sowie von der zugehörigen Kletterfaser.

Zu jeder Purkinjegruppe gehören genau ein positives und ein negatives Kernneuron im Cerebellumkern. Beide Kernneuronen sind Einssignalneuronen und werden von allen Purkinjezellen der zugehörigen Purkinjegruppe gehemmt, wenn diese aktiv sind. Die Hemmung ist relativ und führt zu einer Inversion des Purkinjesignals.

Das positive Kernneuron jeder Purkinjegruppe projiziert erregend vorwiegend in den Thalamus. Das negative Kernneuron jeder Purkinjegruppe projiziert hemmend einerseits in den Nucleus olivaris inferior und unterdrückt dort im Aktivitätsfalle das zugehörige Kletterfasersignal. Andererseits projiziert es im Falle des Nucleus dentatus hemmend zum Nucleus ruber, wo es andere Aufgaben wahrnimmt, die bisher noch nicht beschrieben wurden.

Die positiven, also erregenden Kernneuronen der Kleinhirnkerne sind untereinander durch hemmende (glycinerge) Interneuronen verknüpft, wobei jedes erregende Kernneuron die erregenden Kernneuronen seiner Umgebung hemmt. Die Hemmungsstärke nimmt mit wachsender Feuerrate zu und mit wachsendem Abstand ab. Wir bezeichnen eine solche Hemmung als rezeptive Nachbarhemmung. Sie führt zur Kontrastverstärkung der Signale. Die rezeptive Nachbarhemmung gibt es auch im Thalamus und in der Cortexrinde.

Eine indirekte Projektion des Cortex liefert über die indirekten Moosfasern ein indirektes Cortexsignal zu denjenigen Körnerzellen, deren Parallelfasern ausschließlich die Sternzellen kontaktieren.

Alle Purkinjezellen, die zugehörige Golgizelle und alle Korbzellen einer Purkinjegruppe werden von den primären und sekundären Parallelfasern erregt, wenn diese signalführend sind. Die Körnerzellen der primären Parallelfasern liegen hierbei innerhalb der zugehörigen Purkinjegruppe, die sekundären dagegen außerhalb.

Die synaptische Kopplungsstärke zwischen zwei beliebigen Neuronen des Cerebellums wird mitbestimmt von dem Eintreten der Langzeitpotenzierung beziehungsweise der Langzeitdepression.

Jede Parallelfaser erreicht k Purkinjegruppen, wobei jede Purkinjegruppe eine jede Moosfaser mit einer eigenen Körnerzelle anzapft, ihr Axon bildet die primäre Parallelfaser der Purkinjegruppe. Durch die große Axonlänge der Parallelfasern hat letztlich jede Purkinjegruppe k Parallelfasern, deren Input von der gleichen Moosfaser stammt.

Nach dieser Zusammenfassung aller wesentlichen Details können wir die Funktionsweise des Cerebellums erklären. Dazu bedarf es auch des Einsatzes mathematischen Betrachtungsweisen. Unser Ziel besteht darin, nachzuweisen, dass ein Cerebellumcluster eine sequentielle Kette von Speichereinheiten bildet. Jede Speichereinheit wird durch eine Purkinjegruppe realisiert und kann genau ein Komplexsignal des zugehörigen Cerebellumclusters speichern. Jedes bedeutsame Komplexsignal wird genau einmal gespeichert. Eine Mehrfachabspeicherung wird wirksam verhindert. Die Speicherung erfolgt vollautomatisch und selbständig.

Bereits jetzt soll ein Prüfkriterium aufgestellt werden, an dem die Richtigkeit der noch zu entwickelnden Cerebellumtheorie geprüft werden möge.

Bei den Basalganglien war die evolutionäre Erklärung der acetylcholinergen Projektion der Matrixneuronen in die Striosomenneuronen ein Prüfstein. So ließ sich zeigen, dass diese Projektion aus der Zeit stammt, als es noch gar keine Großhirnrinde gab.

Aus der Literatur ist bekannt, dass es sehr wohl möglich ist, völlig ohne Cerebellum auszukommen. Wer bei seiner Geburt bereits ohne Cerebellum auf diese Welt kam, wird im normalen Leben kaum auffallen, wenn man den Ausführungen verschiedener Neurologen Glauben schenkt. Er wird jedoch nur lebensfähig sein, wenn der Nucleus ruber und die Kleinhirnkerne vorhanden sind. Dies zeigt, dass das Nervensystem das völlige Fehlen der Cerebellumrinde kompensieren kann.

Wer jedoch schon mit funktionierendem Cerebellum geboren wurde, bei dem rufen Störungen im Cerebellum starke und teils lebensbedrohliche Krankheitssymptome hervor. Auf ein bereits benutztes und funktionierendes Cerebellum kann man also nicht verzichten. Hier kann sein Ausfall nicht mehr kompensiert werden.

Genau an dieser Besonderheit wollen wir die hier entwickelte Cerebellumtheorie testen. Es wird sich zeigen, dass der Nucleus ruber und die Cerebellumkerne ein für sich funktionsfähiges Teilsystem sind, welches als „Vorcerebellum“ (Präcerebellum) interpretiert werden kann. Erst später bekam dieses System durch evolutionäre Weiterentwicklung die Cerebellumrinde und wurde damit zum vollständigen Cerebellum.

Wir stellen uns nun den Anfangszustand des Cerebellums vor. Dieser möge gegeben sein, wenn das Cerebellum noch kein einziges Signal erlernt hat, also völlig unwissend ist. Diesen Anfangszustand können wir hypothetisch beschreiben. Dazu benötigen wir jedoch einige elementare Einsichten zur synaptischen Kopplungsstärke zwischen Neuronen.

Theorem 1.32: Theorem der Zwangskopplung von kompatiblen Neuronen im Urzustand

Entwickeln sich in einem Subsystem des Gehirns Proneuronen zu Neuronen, so gehen transmitterkompatible Neuronen zwangsweise eine synaptische Verbindung ein, die im Verlaufe der weiteren Entwicklung modifiziert wird.

Ist das Outputneuron LTP-fähig, so wird als Startwert für die synaptische Kopplung ein Minimalwert k_min gewählt und später durch die einwirkenden Signale erhöht.

Ist das Outputneuron LTD-fähig, so wird als Startwert für die synaptische Kopplung ein Maximalwert k_max gewählt und später durch die einwirkenden Signale vermindert. Theoretisch sind die Startwerte k_min = 0,1 und k_max = 1 brauchbar (ebenso aber z. B. auch k_min = ¹/₂).

Begründung:

Die meisten neuronalen Systeme machen während der Embryonalzeit und auch postnatal eine Entwicklung durch, an deren Anfang sogenannte Proneuronen, also die neuronalen Stammzellen, stehen. Aus ihnen entwickeln sich die verschiedenen Neuronenarten.

Es macht keinen Sinn, Proneuronen zu Neuronen zu entwickeln, wenn diese untereinander keine synaptischen kontakte aufbauen. kontaktaufnahme unter Neuronen ist eine der wichtigsten Aufgaben von Nervenzellen. Transmitterkompatible Neuronen müssen zwangsweise die gegenseitige Verbindung suchen. Die Wegfindung der sich entwickelnden Axone und Dendriten wird von chemischen Stoffen – den sogenannten Markern – gesteuert. Diese bewirken einen Wuchs von Axon und Dendrit entlang des Gradienten der Markerkonzentration. Da die Marker teils selbst von der Axonspitze bzw. der Dendritenspitze erzeugt werden, finden sich beide gegenseitig.

Lediglich die Reichweite der Marker – deren Wirkung mit zunehmender „Verdünnung“ im Medium abnimmt, ist mitverantwortlich für eine begrenzte Reichweite der Axone und Dendriten und somit für die Entstehung von rezeptiven Feldern. Der interessierte Leser möge sich bei Bedarf in der reichlich vorhandenen internationalen Literatur näher informieren.

Wenn LTP als Vorgang zur Erhöhung der synaptischen Stärke führt, ist es sinnvoll, mit einem möglichst kleinem synaptischen Wert zu starten, damit er später erhöht werden kann.

Analog wäre es problematisch, beim Wirksamwerden der LTD mit einem zu kleinem synaptischen Kopplungswert zu starten, da dieser ja gerade durch die LTD verringert werden soll.

Beispielhaft setzen wir die Startwerte und die Endwerte für neurologische Systeme wie folgt fest:

-          Der Minimalwert k_min der Kopplungsstärke für LTP-fähige Outputneuronen sei k_min= 0,5. Er möge sich durch Langzeitpotenzierung auf den Wert k_max = 1 erhöhen.

-          Der Maximalwert k_max der Kopplungsstärke für LTD-fähige Outputneuronen sei k_max= 1,0. Er möge sich durch Langzeitdepression auf den Wert k_min = 0,5 erniedrigen.

Durch Langzeitpotenzierung erhöht sich also die Kopplungsstärke vom Wert ½ auf 1, während sie durch Langzeitdepression vom Wert 1 auf den Wert ½ abfällt. Diese Werte sind realitätsnahe Beispielwerte für diese Monografie.

Weiterhin müssen wir hypothetisch klären, wie die Feuerrate eines Neurons ermittelt wird, welches über n Synapsen mit den Kopplungsstärken k₁, k₂, k₃, …, k_n verfügt, wobei die Inputneuronen die Feuerraten f₁, f₂, f₃, …, f_n besitzen und das Neuron N₁ mit der Feuerrate f₁ die Synapse 1 mit Input versorgt, das Neuron N₂ mit der Feuerrate f₂ die Synapse 2 mit Input beliefert, …, und das Neuron N_n mit der Feuerrate f_n die Synapse n mit Input versorgt.

Definition 1.26: Feuerrate eines Neurons mit mehreren Inputlieferanten bei Analogbetrieb

Es sei N ein Neuron im Analogbetrieb.

Das Neuron N habe n Synapsen, die von den Neuronen N₁, N₂, N₃, …, N_n mit Input beliefert werden. Mit jedem Inputneuron besitze das Outputneuron genau eine Synapse.

Es sei K = (k₁, k₂, k₃, …, k_n) der Kopplungsvektor des Neurons N, wobei k_i die Kopplungsstärke des i-ten Inputneurons sei. Erregender Input zählt positiv, hemmender negativ.

Es sei F = (f₁, f₂, f₃, …, f_n) der zugehörige Vektor der Feuerraten der Inputlieferanten, hier sei f_i die Feuerrate des i-ten Inputneurons.

Dann ergibt sich die Feuerrate f_N des Neurons N aus dem durch die Synapsenanzahl dividierten Skalarprodukt aus dem Kopplungsvektor und dem Feuerratenvektor, wenn diese Zahl nichtnegativ ist, anderenfalls ist diese Feuerrate gleich Null

       f_N = K _* F / n,  wenn (K _* F / n) = 0             (normiertes Skalarprodukt)

       f_N = 0,             wenn (K _* F / n) < 0.

Mit d(x) = x für x = 0 und d(x) = 0 für x < 0 (Haeviside-Funktion) gilt:

       f_N = d[(k₁*f₁ + k₂ * f₂ + k₃ * f₃ + … + k_n * f_n) / n].

Bemerkung:

Es gibt nur nichtnegative Feuerraten als Ergebnis des Zusammenwirkens von Erregung und Hemmung.

Neben dem Analogbetrieb gibt es bei Neuronen noch den Binärbetrieb und den Phasenbetrieb. Die Purkinjezellen im Cerebellum arbeiten nach Ansicht des Autors dieser Monografie im Analogbetrieb.

Definition 1.26 berücksichtigt lediglich die allseits bekannte Erscheinung, dass die Wirkung einer Synapse umso geringer ausfällt, je mehr Synapsen ein Neuron besitzt. In diesen Fällen ist (zu mindestens vereinfacht) die Synapsenwirkung einer einzelnen Synapse indirekt proportional zur Gesamtanzahl der Synapsen.

Es ist unklar, ob diese einfache Rechenweise realitätsnah ist. Sie unterstellt bei Neuronen im Analogbetrieb eine Linearität. Dies ist die stärkste Vereinfachung bei Neuronenmodellen. Sie hat jedoch den Vorteil der leichten Verständlichkeit.

Nunmehr können wir die Kopplungsstärken des Urzustandes im Cerebellum präziser fassen.

 

Theorem 1.33: Kopplungsstärken des Urzustandes im Cerebellum

 

Die Purkinjezellen des Cerebellums sind LTD-fähig.

Die Sternzellen, Korbzellen, Golgizellen sowie die Kernneuronen sind LTP-fähig.

Nachfolgende Tabelle gibt (in grober Näherung) die synaptische Kopplungsstärke k jeder dieser Zellarten zu einem der beteiligten Neuronen in ungeprägten und im geprägten Zustand an:

 

Zellart	Ungeprägt	Geprägt	Wirkung	Prägungsart
Moosfaser/pos. Kernneuron	kMF/KN+ = 0,5	kMF/KN+ = 1	errregend	LTP
Moosfaser/neg. Kernneuron	kMF/KN- = 0,5	kMF/KN- = 1	erregend	LTP
Parallelfaser/Purkinjezelle	kPF/PZ = 1	kPF/PZ = 0,5	erregend	LTD
Parallelfaser/Korbzelle	kPF/KZ = 0,5	kPF/KZ = 1	erregend	LTP
Parallelfaser/Sternzelle	kPF/SZ  = 0,5	kPF/SZ  = 1	erregend	LTP
Parallelfaser/ Golgizelle	kPF/GZ = 0,5	kPF/GZ = 1	erregend	LTP

Die übrigen Synapsen im Cerebellum und den Cerebellumkernen sind nicht notwendigerweise durch LTP oder LTD veränderlich. Sie haben daher keinen Kletterfaserkontakt und sind in ihrer Kopplungsstärken konstant gemäß nachfolgender Tabelle:

 

Zellart	Kopplungsstärke	Wirkung
Moosfaser/Körnerzelle	kMF/KZ = 1	erregend
Golgizelle/Moosfaser	kGZ/MF = - 1	hemmend
Sternzelle/Purkinjezelle	kSZ/PZ = -1	hemmend
Korbzelle/Purkinjezelle	kKZ/PZ = -1	hemmend
Purkinjezelle/pos. Kernzelle	kPZ/KZ+ = - 1	hemmend
Purkinjezelle/neg. Kernzelle	kPZ/KZ- = - 1	hemmend
Moosfaser/pos. Kernzelle	kMF/KZ+ = + 1	erregend
Moosfaser/neg. Kernzelle	kMF/KZ- = + 1	erregend
Kletterfaser/Purkinjezelle	kKF/PZ = 300	erregend
Kletterfaser/Sternzelle	kKF/SZ = 1	erregend
Kletterfaser/Korbzelle	kKF/KZ = 1	erregend
Kletterfaser/Golgizelle	kKF/GZ = 1	erregend

                                                                                 

(Ende des Theorems)

Die synaptische Wirkung der Kletterfaser auf die Purkinjezelle wurde wegen der starken Wirkung (willkürlich) mit 300 bewertet, da es etwa 300 Synapsen dieses Axons mit der Purkinjezelle gibt.

Ebenso wurde die Kletterfaserwirkung auf die übrigen Interneuronen des (willkürlich) mit 1 angesetzt.

An dieser Stelle sei es dem Autor gestattet, von der ursprünglichen ersten Fassung dieser Monografie vom 15.08.2011 stärker abzuweichen. Neue Einsichten erforderten eine Neufassung des gesamten Kapitels 1.7 und eine Zusammenlegung mit dem ehemaligen Kapitel 1.8. Genau diese neuen Einsichten mögen nunmehr erläutert werden.

Im Zuge der theoretischen Analyse der Kopplungsverhältnisse im Cerebellum bemerkte der Autor die bereits in Theorem 1.27. postulierte Arbeitsteilung zwischen Korbzellen und Sternzellen.

In den obigen Tabellen zu den Kopplungsfaktoren fällt auf, dass es eine Hemmung der Purkinjezelle durch zwei Zellarten des Cerebellums gibt. Einerseits werden die Purkinjezellen von den Korbzellen gehemmt. Letztere haben einen größeren Dendritenbaum. Ebenso werden die Purkinjezellen von den Sternzellen gehemmt. Diese haben kleinere Dendritenbäume. Sowohl Korbzellen als auch Sternzellen werden von den Parallelfasern erregt.

Damit können wir die synaptische Gesamtkopplung berechnen.

Bevor wir jedoch die Prägung – also den Lernprozess im Cerebellum – mathematisch fassen, müssen wir klären, was denn ein Prägungssignal sein soll.

Wir beginnen mit dem mathematischen Begriff des Prägungsvektors.

Langzeitdepression und Langzeitpotenzierung im Cerebellum benötigen die tetanische (höherfrequente) Erregung durch das Kletterfasersignal. Aber auch die Parallelfasersignale müssen eine gewisse und hinreichend starke Erregung aufweisen, damit die Synapse zwischen ihnen und den Purkinjezellen, Korbzellen, Golgizellen und Kernzellen von ungeprägten Urzustand in den geprägten Zustand überführt werden kann.

Daher fordern wir, dass die signalliefernden Neuronen des betreffenden Cortexclusters eine relativ hohe Feuerrate aufweisen, damit LTP bzw. LTD erzeugt wird, wodurch die betreffende Zelle geprägt wird und dieses Signal als das ihrige erkennt. Wir wollen den erforderlichen Mindestwert der Feuerrate als Prägungs-Feuerrate bezeichnen und durch das Symbol f_p darstellen. Ebenso nötig ist eine hinreichend lange gleichzeitige Einwirkung einer tetanischen Erregung über die Kletterfaser als auch über die Parallelfasern. Wir fordern eine solche Mindest-Einwirkzeit von einer Sekunde.

Die Prägungs-Feuerrate bestimmt also, ob ein Cortex-Signalneuron mit seinem Output in das Prägungssignal eines Cerebellumneurons einbezogen wird oder nicht. Daher können wir den Begriff Prägungssignal präzisieren. Erreicht ein Signalneuron nicht die erforderliche Prägungsgfeuerrate f_p, so kann es an den zugehörigen Parallelfasern keine LTP oder LTD bewirken.

Definition 1.27: (Binärer) Prägungsvektor eines Signalvektors

Es sei F = (f₁, f₂, f₃, …, f_n) der Vektor der Feuerraten der n (direkten und indirekten) Signalneuronen, hierbei sei f_i die Feuerrate des i-ten Signalneurons.

Weiterhin sei f_p die Prägungs-Feuerrate.

Dann bezeichnen wir den lediglich aus Nullen und Einsen bestehenden Vektor

       P = (d₁, d₂, d₃, … , d_n)

als (binären) Prägungsvektor, wobei die Werte d₁, d₂, d₃, … , d_n unter Berücksichtigung der Prägungs-Feuerrate f_p zu bestimmen sind:

       d₁ = 0, falls f₁ < f_p, sonst d₁ = 1, aber nur, wenn f₁ mindestens 1 s andauert

       d₂ = 0, falls f₂ < f_p, sonst d₂ = 1, aber nur, wenn f₂ mindestens 1 s andauert

       d₃ = 0, falls f₃ < f_p, sonst d₃ = 1, aber nur, wenn f₃ mindestens 1 s andauert

       …. usw…,

       d_n = 0, falls f_n < f_p, sonst d_n = 1, aber nur, wenn f_n mindestens 1 s andauert.

Die Zeitmessung zur Ermittlung der Mindestdauer der beteiligten Signale beginnt für alle Signalneuronen gleichzeitig. Alle Signale, deren Dauer nicht ab Start wenigstens eine Sekunde beträgt, fallen aus dem Prägungssignal heraus.

Ist also die Feuerrate f_i des i-ten Cortexneurons kleiner als die Prägungs-Feuerrate fp, so ist die zugehörige Komponente im (binären) Prägungsvektor gleich Null, anderenfalls gleich Eins, vorausgesetzt, diese Feuerrate wird mindestens eine Sekunde lang realisiert.

Die Mindest-Einwirkzeit für die Entstehung von LTP bzw. LTD soll hier (beispielhaft) eine Sekunde lang sein.

Beispiel:

Wir wählen vereinfachend nur 5 Neuronen N₁, N₂, N₃, N₄, N₅. Die zugehörigen Feuerraten seinen f₁ = 200, f₂ = 10, f₃ = 70, f₄ = 35, f₅ = 110. Weiterhin sei die Prägungs-Feuerrate beispielhaft gleich 50, also f_p = 50. Jede Feuerrate dauere wenigstens eine Sekunde an.

Dann hat der zugehörige Prägungsvektor P₅ folgendes Aussehen:

            P₅ = (1, 0, 1, 0, 1).

Denn f₁, f₃ und f₅ sind größer als 50, und f₂ sowie f₄ sind kleiner als 50. Hier wurden nur 5 Neuronen gewählt, damit das Beispiel übersichtlich bleibt. Im Cortexcluster gibt es jedoch mehrere hundert ( oder gar tausend) Cortexneuronen.

Bei stetigen Signalen wäre eine Definition des Prägungsvektors über ein Zeitintegral möglich. Wenn das Zeitintegral der Signalstärke eines Signalneurons über einem Zeitintervall einen Mindestwert übersteigt, wäre die Vektorkomponete des Prägungsvektors gleich 1, ansonsten Null. Da aber die Aktionspotentiale letztlich als diskrete Ereignisse auch einfach gezählt werden können, ist die Anzahl der Aktionspotentiale pro Zeiteinheit gleichwertig. Dem ebenso fast gleichwertig ist eine Mindestfeuerrate, wie sie hier gewählt wurde.

An dieser Stelle sollte kurz erläutert werden, warum der Prägungsvektor das Attribut „binär“ erhalten hat. Es hat etwas mit binärer Arithmetik zu tun, die wir vorwiegend bei Computern antreffen. Es ist daher sinnvoll, dem binären Prägungsvektor auch eine binäre, genauer eine Dualzahl zuzuordnen. Sie möge dadurch gebildet werden, dass wir die einzelnen Komponenten des Prägungsvektors als Dualziffern einer Dualzahl interpretieren. Dieser Zahl werden wir einen charakteristischen Namen geben und sie als Signatur des Prägungssignals bezeichnen.

Definition 1.28: Signatur eines Prägungssignals

Diejenige Dualzahl, deren Dualziffern (unter Einhaltung ihrer Reihenfolge) den Komponenten des Prägungsvektors zu einem Prägungssignal entsprechen, bezeichnen wir als Signatur des Prägungssignals.

Die Signatur ist eine natürliche Zahl. Als Dualzahl besitzt sie so viele Dualziffern, wie das Signal Komponenten besitzt. Damit ist die Anzahl der Dualziffern gleich der Anzahl der Neuronen, die dieses Signal bilden.

Ist die Feuerrate der k-te Komponente des Signals kleiner als die Prägungsfeuerrate oder hält nicht wenigstens eine Sekunde an, so ist die Feuerrate des Prägungssignals gleich Null, ebenso ist die k-te Dualziffer gleich Null.

Unter Zuhilfenahme des (binären) Prägungsvektors können wir nun das Prägungssignal ermitteln.

Definition 1.29: Prägungssignalvektor

Das Prägungssignalvektor S_P zu einem Signalvektor S ergibt sich als Vektorprodukt des (binären) Prägungsvektors P mit dem Signalvektor S:

P = (d₁, d₂, d₃, … , d_n)       d_i aus {0, 1} für alle i

S = (f₁, f₂, f₃, ..., f_n).

S_P = (d_1* f₁, d_{2 *} f₂, d_{3 *} f₃, … , d_{n *} f_n)                  (Prägungssignalvektor).

Vereinfacht geht der Prägungssignalvektor aus dem Signalvektor dadurch hervor, dass alle Feuerraten, die kleiner als die Prägungs-Feuerrate f_p sind, durch die Zahl Null ersetzt werden. Ebenso werden alle Feuerraten, die nicht wenigstens eine Sekunde lang andauern, gleich Null gesetzt. Hierbei beginnt die Zeitmessung der einen Sekunde für alle beteiligten Neuronen gleichzeitig.

Unser weiteres Vorgehen soll einer gewissen Systematik folgen. Zunächst berechnen wir die Signalverhältnisse im ungeprägten Cerebellum. Dieser liegt vor, wenn das Cerebellum sich im Urzustand befindet und noch keinerlei Signale erlernt hat.

Wir erinnern uns, dass die Signale des Cortexclusters über die Brückenkerne die direkten Moosfasern mit dem direkten Cortexsignal versorgen, die wiederum die direkten Moosfasern mit Input versorgen. Von diesen werden die direkten Parallelfasern gespeist, die ihrerseits sowohl die Purkinjezellen als auch die Korbzellen sowie die Golgizellen erregen, aber auch die zugehörigen Kernneuronen. Damit ist all diesen Neuronen zunächst einmal der direkte Signalvektor S_D zugeordnet, der aus n Signalneuronen des Cortexclusters besteht:

            S_D = (f_D,1; f_D,2; f_D,3; ..., f_D,n).

Hierbei ist f_D,i die Feuerrate des i-ten Signalneurons des Cortexclusters. Die Signalstärke dieses Signals ergibt sich als Mittelwert der beteiligten Signalstärken:

            f_D = (f_D,1 + f_D,2 + f_D,3 + ... + f_D,n)/n.

Der indirekte Signalvektor S_i bestehe aus m Komponenten gemäß

            S_i = (f_i,1; f_i,2; f_i,3; ...; f_i,m).

Die Signalstärke (Feuerrate) des indirekten Signals ergibt sich zu

            fi = (f_i,1 +  f_i,2 + f_i,3 + ... + f_i,m)/m.

 

Wir bilden den Vektor des Gesamtsignals S als Vektorsumme, die nun aus n + m Vektorkomponenten besteht, von denen die ersten dem direkten Signalvektor und die letzten m dem indirekten Signalvektor entsprechen.

            S = (f_D,1; f_D,2; f_D,3; ..., f_D,n; f_i,1; f_i,2; f_i,3; ...; f_i,m).

 

Die (theoretische) Feuerrate f ergibt sich durch Mittelwertbildung über den (n+m) Summanden.

            f = [(f_D,1 + f_D,2 + f_D,3 + ... + f_D,n) + (f_i,1 +  f_i,2 + f_i,3 + ... + f_i,m)]/(n+m).

            f = f_d/(n+m) + f_i/(n+m).

            f = p_*f_D + q_*f_i.    (Signalstärke des Gesamtinputs aus direktem und indirektem Signal)

Hierbei gilt p + q = 1 und p/q = n/m.

Das Kletterfasersignal zählen wir hier nicht mit, da es ja nicht erlernt werden soll. Erlernt werden soll nur die aktuelle Signalkombination aus direktem und indirektem Signal. Das Kletterfasersignal wirkt zwar auf das zu prägende Neuron ein, aber nur zur Auslösung der Langzeitdepression bzw. Langzeitpotenzierung. Je mehr verschiedene Signale ein Cerebellumcluster erlernt hat, umso mehr Signale wird es erkennen und im Erkennungsfalle die Kletterfasersignale unterdrücken. So werden aktive Kletterfasersignale im Laufe der Zeit immer seltener, am Ende sind es quasi Raritäten.

Nunmehr erinnern wir uns an den Prägungsprozess. Diejenigen Komponenten eines Signalvektors, deren Feuerrate für die (als Beispiel) vorgegebene Zeitdauer von einer Sekunde mindestens die Prägungsfeuerrate erreichten, wurden dem Prägungssignal zugeordnet. Die übrigen Vektorkomponenten ordnen wir dem Restsignal zu. Damit kann der Inputvektor als Summe aus dem Prägungssignal und dem Restsignal dargestellt werden.

            S = S_P + S_R.

 

Da aber das Signal S bereits eine Vektorsumme aus direktem und indirektem Signal ist, besteht der Signalvektor aus 4 Summanden:

            S = S_DP + S_DR + S_iP + S_iR.

 

Das direkte Signal S_D besteht nunmehr aus einem Prägungsanteil und einem Fremdsignalanteil, gleiches gilt für das indirekte Signal S_i. Es ist zu erwähnen, dass alle vier Vektoren linear unabhängig sind.

Dieser Inputvektor erreicht über die Moosfasern das Cerebellum. Dies liegt in der vereinfachenden Annahme begründet, jedes Signalneuron des direkten Cortexsignals projiziere über genau ein Brückenkernneuron auf eine Moosfaser, wobei sich die Feuerrate nicht ändern möge. Analoges gelte für die indirekten Signalneuronen der Formatio reticularis und des magnocellularen Mittelwertsystems.

Am einfachsten berechnen sich die Feuerraten der positiven und negativen Kernneuronen. Hier unterscheiden wir den ungeprägten und den geprägten Zustand dieser Neuronen. Prägungsursache ist das Kletterfasersignal, welches diese Neuronen kontaktiert. Hier nehmen wir vereinfachend nachfolgendes Theorem an:

Theorem 1.34: Eindeutige Zuordnung der Kletterfasern zu den Kernneuronen

Jede Kletterfaser kontaktiert genau ein positives (glutamaterges) Kernneuron des zugehörigen Kleinhirnkerns. Ebenso kontaktiert jede Kletterfaser genau ein negatives (GABAerges) Kernneuron des zugehörigen Kleinhirnkerns.

Damit tragen die Kletterfasern nicht mehr zur Einssignalerregung der Kernneuronen bei. Sie dienen ausschließlich der Prägung der Kernneuronen mit dem Prägungssignal. Wir werden später sehen, dass die Kletterfasersignale zum großen Teil gehemmt werden, wenn die Signalerkennung stattfindet. Daher vernachlässigen wir deren Signalanteile bei der Berechnung, wo es angebracht zu sein scheint.

Die Feuerrate der ungeprägten Kernneuronen ist gleich der halben Feuerrate f des Gesamtsignals S. Denn jede Synapse der Kleinhirnkernneuronen hat laut Vorgabe die synaptische Kopplungsstärke ½.

            f_KN,u = ½ f                   (Feuerrate des ungeprägten Kernneurons).

Dies gilt, weil die einzelnen Signalkomponenten des Inputvektors

            S = (f_D,1; f_D,2; f_D,3; ..., f_D,n; f_i,1; f_i,2; f_i,3; ...; f_i,m).

 

mit dem Kopplungsvektor

            K = (½; ½; ½; ...; ½)    n + m Komponenten

skalar multipliziert werden. Jede Feuerrate wird mit dem zugehörigen Kopplungswert ½ multipliziert, die Summe gebildet und durch (n+m) dividiert. Das Ergebnis ist genau die Hälfte der Feuerrate f des Gesamtinputs:

            f_KN,u = (½ f_D,1 + ½  f_D,2 + ½ f_D,3 + ... + ½ f_D,n + ½ f_i,1 + ½ f_i,2 + ½ f_i,3 +  ...; + f_i,m)/(n+m)

            f_KN,u = ½ f.

Bei der Feuerrate des geprägten Kernneurons werden bei den prägungsfähigen Komponenten des Signals die synaptischen Kopplungsstärken durch LTP vom Wert ½ auf den Wert 1 erhöht. Daher gehen die Vektorkomponenten der Prägungssignalvektor mit dem Wert 1 in die neue Feuerrate ein, während die des Restsignalvektors mit der Kopplungsstärke ½ berücksichtigt werden. Diese Gesamtfeuerrate des Inputvektors war in den direkten und indirekten Anteil zerlegt worden.

f = p_*f_D + q_*f_i.

Der Inputvektor besteht nunmehr aus direktem und indirektem Prägungssignal und direktem und indirektem Restsignal:

            S = S_DP + S_DR + S_iP + S_iR.

 

Der Komponenten des direkten Prägungssignals S_DP und ebenso des indirekten Prägungssignals S_iP besitzen mindestens die Prägungsfeuerrate f über einen Prägungszeitraum von einer Sekunde (Beispielwert) und wirken während der Prägung gleichzeitig mit dem tetanischen Kletterfasersignal auf das Kernneuron ein. Dadurch steigt die synaptische Kopplungsstärke vom bisherigen Wert ½ auf den Wert 1.

Die Synapsen der Inputaxone zum direkten und indirekten Restsignal behalten ihre bisherige Kopplungsstärke von ½.

Ausmultiplizieren, Summieren und Dividieren durch die Synapsenanzahl (n + m) liefert die Feuerrate für das geprägte Kernneuron.

Jede Komponente des Prägungssignals geht mit dem Faktor 1 in die resultierende Feuerrate des geprägten Neurons ein, die Restsignalkomponenten mit dem Faktor ½. Daher gilt für die Feuerrate des geprägten Kernneurons die Gleichung

            f_KN,g = p * (f_dP + ½ f_dR) + q * ( f_iP + ½ f_i,R)    (Feuerrate geprägtes Kernneuron).

            f_KN,g = ½ f + ½ f_P

Hierbei ist f_P die Signalstärke des Prägungssignals, also die mittlere Feuerrate des Prägungsanteils.

Theorem 1.35: Feuerrate der Kernneuronen

Ist f die Feuerrate des Gesamtinputs (ohne Kletterfasereinwirkung) und f_P die mittlere Signalstärke des Prägungssignals, so hat ein ungeprägtes Kernneuron die Feuerrate

       f_KN,u = ½ f                   (Feuerrate des ungeprägten Kernneurons),

während ein geprägtes Kernneuron die Feuerrate

            f_KN,g = ½ f + ½ f_P        (Feuerrate des geprägten Kernneurons),

besitzt.

Aus dem obigen Theorem lässt sich ableiten, dass die geprägten positiven (glutamatergen) und negativen (GABAergen) Neuronen der Kleinhirnkerne bereits ihre Prägungssignale mit deutlich stärkerem Output in Richtung Thalamus bzw. Olive oder Nucleus ruber senden.

Da im Thalamus nur hemmende Interneuronen vorhanden sind, hemmt dasjenige Neuron, welches den stärksten Input erhält, alle benachbarten. Daher setzt sich jeweils das stärkste Signal im Thalamus durch und informiert dann den Cortex darüber, dass das zugehörige Kernneuron im Cerebellumkern sein Prägungssignal erkannt hat.

Das zugehörige negative (hemmende) Kernneuron hemmt dagegen in der Olive bzw. im Nucleus ruber das Kletterfasersignal und verhindert so die Prägung anderer, freier Kernneuronen mit dem bereits erlernten Signal.

Nach dieser Erkenntnis wollen wir das Gebiet des Thalamus, in welches die positiven Kernneuronen eines Cerebellumclusters projizieren, als zugehöriges Thalamuscluster bezeichnen.

Definition 1.30: Thalamuscluster

Das Gebiet des Thalamus, in welches die positiven Kernneuronen eines Cerebellumclusters projizieren, bezeichnen wir als zugehöriges Thalamuscluster.

Daher gilt das nachfolgende Theorem.

Theorem 1.36: Die Kleinhirnkerne als Speichersystem für Prägungssignale

Die Cerebellumkerne sind auch ohne Cerebellumrinde lernfähig und in der Lage, Prägungssignale durch LTP zu erlernen. Sie sind also mit Speicherschaltkreisen vergleichbar. Der neuronale Schreibbefehl ist das Kletterfasersignal. Die erregenden Kernneuronen informieren den Thalamus über die Signalerkennung, wobei sich wegen der rezeptiven Nachbarhemmung im Kleinhirnkern und im zugehörigen Thalamuscluster die Signale der Neurons durchsetzen, deren Prägungssignal die beste Übereinstimmung mit dem aktuell anliegenden Signal besitzt. Die hemmende Projektion der negativen Kernneuronen zum Nucleus olivaris inferior hemmt die Kletterfasersignale im Aktivitätsfall und verhindert so die Mehrfachprägung von Signalen in den Cerebellumkernen.

Nun wird klarer, warum das Cerebellum nicht unbedingt lebensnotwendig ist. Wer von Geburt an kein Cerebellum besaß, aber über funktionsfähige Kleinhirnkerne und eine funktionsfähige Olive sowie einen funktionierenden Nucleus ruber verfügte, konnte ein unauffälliges Leben führen. Nach Angaben von führenden Neurologen sind Menschen mit völlig fehlendem Kleinhirn oftmals erst bei notwendigen medizinischen Untersuchungen erkannt worden.

Wer aber mit vollständigem Kleinhirn geboren wurde, kann den Ausfall des Cerebellums nicht mehr problemlos kompensieren. Hier sind schwerwiegende Komplikationen und lebensgefährliche Symptome zu erwarten, wenn das Cerebellum massiv geschädigt wird.

Dennoch ergibt sich die Frage, wozu denn die Cerebellumrinde entstand, wo es doch ohne sie ganz gut funktionierte. Hier müssen wir weiter ins Detail gehen und die Beiträge der Cerebellumneuronen zur Gesamtfunktion analysieren.

Zuvor sollten wir aus systemtheoretischen Gründen und zur Vermeidung von Verwechslungen den Begriffen Prägungssignal und Restsignal sinnvolle Entsprechungen zuweisen.

Definition 1.31: Eigensignal, Fremdsignal und Signatur eines Neurons

Wird ein Neuron vermittels LTP mit einem Prägungssignal geprägt, so nennen wir dieses Prägungssignal das Eigensignal des Neurons. Der nicht zum Eigensignal gehörende Anteil eines beliebigen Inputsignals für dieses Neuron wird als Fremdsignal dieses Neurons bezeichnet. Durch die Prägung wird die Signatur des Prägungssignals zur Signatur des Eigensignals und zur Signatur dieses Neurons.

Prägungssignal und Restsignal sind Begriffe, die die verschiedenen Inputsignalanteile des Cerebellums präzisieren.

Das Eigensignal ist eine Systemeigenschaft eines Neurons, die durch die Prägung induziert wird. Verschiedene Neuronen haben im Allgemeinen verschiedene Eigensignale und damit auch verschiedene Signaturen. Dies hängt mit dem Algorithmus zusammen, der im Cerebellum die Mehrfachprägung verschiedener Neuronen mit dem gleichen Prägungssignal verhindert.

Nunmehr können wir die Feuerrate der Korbzellen berechnen. Diese sind prägungsfähig, unterliegen der Langzeitpotenzierung und erhalten ausschließlich den Input des direkten Cortexsignals. Wir vernachlässigen die mögliche Signalstärke des Kletterfasersignals.

Jedes Signalneuron des Cortexclusters projiziert in eine Moosfaser. Diese beliefert etwa w = 400 Parallelfasern mit ihrer Feuerrate, die dadurch auch zur Feuerrate der w = 400 Parallelfasern wird. Diese bilden pro Moosfaser w = 400 Synapsen mit der Korbzelle.

Aber auch die Synapsenanzahl der Korbzelle ist w = 400-mal größer als die Anzahl der Moosfasern. Zur Berechnung der Feuerrate der Korbzelle sind die Feuerraten der Parallelfasern (die gleich der Feuerraten der zugehörigen Moosfasern und somit gleich den Feuerraten der Cortexneuronen sind), mit der synaptischen Kopplungsstärke zu multiplizieren und aufzusummieren. Die Gesamtsumme wird durch die Gesamtanzahl der Synapsen dividiert.

Die ungeprägte Korbzelle hat in jeder Synapse die Kopplungsstärke ½. Daher gilt für die Feuerrate f_KO die Gleichung

            f_KO,U = ( w_* ½ _* f_D1 + w _* ½ _* f_D2 + w _* ½ _* f_D3 + ... + w _* ½ _* f_Dn) / ( w _* n)

Der Faktor w = 400 lässt sich herauskürzen. Damit ergibt sich die Feuerrate der ungeprägten Korbzelle zu

            f_KO,U = ½ f_D                (die Feuerrate der ungeprägten Korbzelle):

Wir erkennen, dass die Feuerrate der ungeprägten Korbzelle identisch ist mit der halben Feuerrate des direkten Cortexsignals.

Dies ist in gewisser Weise logisch, da jede Synapse der Korbzelle den Kopplungswert ½ besitzt, so dass die Cortexsignale letztlich nur mit der halben Gesamtstärke auf die Korbzelle einwirkt.

Nun berechnen wir die Feuerrate der Korbzelle nach ihrer Prägung mit dem Prägungssignal.

Hierbei besteht das direkte Cortexsignal aus dem direkten Prägungsanteil S_DP und dem direkten Restsignalanteil S_DR.

S = S_DP + S_DR

Vor der Prägung hatten alle Synapsen der Korbzelle den Kopplungswert ½. Nach der Prägung durch das Kletterfasersignal haben alle Synapsen, die vom Prägungssignalvektor geprägt wurden, ihre synaptische Kopplungsstärke vom Wert ½ auf den Wert 1 erhöht. Die zugehörige Änderung in den Berechnungsformeln für die Feuerrate f_KO,G der geprägten Korbzelle sind so einfach, dass wir nur das Endergebnis angeben.

            f_KO,G = f_DP + ½ f_DR.

            f_KO,G = ½ f_D + ½ f_DP.

            f_KO,G = f_KO,U + ½ f_DP.              (Feuerrate der geprägten Korbzelle)

 

Daher gilt das nachfolgende Korbzellentheorem.

 

Theorem 1.37: Korbzellentheorem

 

Ohne Kletterfasersignaleinwirkung hat die ungeprägte Korbzelle die halbe Feuerrate des direkten Cortexsignals. Durch die Prägung erhöht sich diese Feuerrate um die halbe Feuerrate des direkten Eigensignals dieser Korbzelle.

Die Berechnung der Feuerrate der ungeprägten bzw. der geprägten Sternzelle ohne Kletterfasersignaleinwirkung läuft analog. Jedoch empfangen die Sternzellen über ihre Parallelfasern ausschließlich das indirekte Cortexsignal des aufmerksamkeitssteuernden Systems. Daher nimmt das indirekte Cortexsignal hier den Platz des direkten Cortexsignals ein.

Wegen der Einfachheit dieser Berechnung geben wir nur das Ergebnis an.

            f_SZ,U = ½ f_i                  (die Feuerrate der ungeprägten Sternzelle):

            f_SZ,G = f_iP + ½ f_iR.

            f_SZ,G = ½ f_i + ½ f_iP.

            f_SZ,G = f_SZ,U + ½ f_iP.                (Feuerrate der geprägten Sternzelle)

 

Theorem 1.38: Sternzellentheorem

 

Ohne Kletterfasersignaleinwirkung hat die ungeprägte Sternzelle die halbe Feuerrate des indirekten Cortexsignals. Durch die Prägung erhöht sich diese Feuerrate um die halbe Feuerrate des aktuellen indirekten Eigensignals dieser Sternzelle.

In den obigen zwei Theoremen wurden die Begriffe direktes Eigensignal und indirektes Eigensignal benutzt. Wenn das Cortexsignal aus einen direkten und einem indirekten Signalanteil besteht, so lässt sich das Eigensignal auch in einen direkten und einen indirekten Eigensignalanteil zerlegen. Der direkte Eigensignalanteil wirkt an den Synapsen zwischen Parallelfasern und Korbzellen, der indirekte an den Parallelfasern und den Sternzellen, wobei als Input das Eigensignal nötig ist.

Als nächstes ermitteln wir die Feuerrate der ungeprägten und der geprägten Golgizellen. Wir gehen davon aus, dass diese nur vom direkten Cortexsignal erreicht werden, was auch für die Korbzellen zutrifft. Und ebenso wie die Korbzellen unterliegen auch die Golgizellen der Langzeitpotenzierung, wozu sie direkten Kletterfaserkontakt haben. Daher ist die Feuerrate der ungeprägten Goligzellen identisch mit der Feuerrate der ungeprägten Korbzellen. Ebenso ist die Feuerrate der geprägten Golgizellen identisch mit der Feuerrate der geprägten Korbzellen.

            f_GO,G = f_DP + ½ f_DR.

            f_GO,G = ½ f_D + ½ f_DP.

            f_GO,G = f_GO,G + ½ f_DP.              (Feuerrate der geprägten Golgizelle)

 

Daher gilt das nachfolgende Golgizellentheorem.

 

Theorem 1.39: Golgizellentheorem

 

Ohne Kletterfasersignaleinwirkung hat die ungeprägte Golgizelle die halbe Feuerrate des direkten Cortexsignals. Durch die Prägung erhöht sich diese Feuerrate um die halbe Feuerrate des direkten Eigensignals dieser Golgizelle.

Nunmehr berechnen wir die Feuerrate der ungeprägten und danach der geprägten Purkinjezelle. Diese empfängt den erregenden Input des direkten und indirekten Cortexsignals über die Parallelfasern sowie den hemmenden Input aus der zugehörigen spezifischen Korbzelle und der zugehörigen spezifischen Sternzelle.

Wir entschließen uns, einer Eingebung folgend zunächst den erregenden Input der Purkinjezelle zu berechnen. Er ergibt eine positive Erregungsfeuerrate. Anschließend subtrahieren wir den hemmenden Input der Korb- und der Sternzelle, um die Endfeuerrate zu ermitteln. Dies liegt in der Annahme begründet, die Hemmung durch Korb- und Sternzelle könnte die aufgebaute positive Erregung völlig hemmen, so dass die Purkinjezelle damit signallos wird.

Wir erinnern uns daran, dass nach dieser Theorie die Synapsen der Parallelfasern mit der Purkinjezelle der Langzeitdepression unterliegen. Daher ist der Startwert der synaptischen Kopplung vor der Prägung gleich 1 und fällt nach der Prägung auf den Wert ½.

Somit gilt für die Feuerrate der ungeprägten Purkinjezelle ohne Hemmungseinwirkung durch Korb- bzw. Sternzelle die Gleichung

            f_PZ,U+ = ( 1 _* w _* f_D1 + 1 _* w _* f_D2 + 1 _* w _* f_D3 + ... + 1_* w _* f_Dn

 

                               + 1 _* w _* f_i1 + 1 _* w _* f_i2 + 1 _* w _* f_i3 + ... + 1_* w _* f_im) / [ w _* (n+m)]

Die erste Summe stellt das von den Parallelfasern überbrachte direkte Cortexsignal dar,

die zweite das indirekte Cortexsignal.

Der Faktor w kürzt sich heraus und erhalten

            f_PZ,U+ = (f_D1 + f_D2 + f_D3 + ... + f_Dn

 

                               + f_i1 + f_i2 + f_i3 + ... + f_im) / [ (n+m)]

Dies ist jedoch genau der Ausdruck für das Gesamtsignal S und dessen Feuerrate f.

Damit ist die Feuerrate der ungeprägten Purkinjezelle ohne Einwirkung von Korb- bzw. Sternzelle identisch mit der Feuerrate des Gesamtsignals aus direktem und indirektem Cortexsignal.

            f_PZ,U+ = f = p _* f_D + q _* f_i.       (Feuerrate der ungeprägten Purkinjezelle ohne den

                                                           hemmenden Einfluss von Korb- und Sternzelle)

Davon wäre nun die Feuerrate der Korb- und der Sternzelle zu subtrahieren, wenn wir vereinfachend Linearität voraussetzen. Angesichts der Tatsache, dass p + q = 1 ergibt, werden wir die Korbzelle mit dem Kopplungsfaktor p und die Sternzelle mit dem Kopplungsfaktor q wirken lassen, so dass ihre Gesamtkopplung auch 1 ergibt.

Dann ergibt sich

            f_PZ,U = p _* f_D + q _* f_i – p _* ½ f_D – q _* ½ f_i.

Daraus folgt

            f_PZ,U = p _* ½ f_D + q _* ½ f_i = ½ f.

            f_PZ,U = ½ f                   (Feuerrate der ungeprägten Purkinjezelle mit Berücksichtigung

der Hemmung durch die zugehörige Korbzelle und Sternzelle)

Die ungeprägte Purkinjezelle feuert also mit der halben Feuerrate des Gesamtinputs, wenn sie von den Parallelfasern erregt und von der ungeprägten Korb- und Sternzelle gehemmt wird.

Nun werden wir die Feuerrate der Purkinjezelle berechnen, die ausschließlich durch den erregenden Einfluss der Parallelfasern nach der Prägung hervorgerufen wird. Wir erinnern uns, dass die prägenden Anteile des Prägungssignals an den Synapsen der Purkinjezellen zur deutlichen Verminderung der synaptischen Kopplung führen, weil die Langzeitdepression wirksam wird. Genau diese Synapsen werden aber mit dem Prägungssignal beliefert. Die Kopplungsstärke für die Restsignalanteile bleibt beim Wert 1, da weder die Feuerrate noch ihre Einwirkungsdauer für die Prägung ausreichen.

Den Input für die geprägte Purkinjezelle liefert das Gesamtsignal S aus direktem und indirektem Cortexsignal mit dem jeweiligen Prägungssignal und dem dazugehörigen Restsignal:

            S = S_DP + S_DR + S_iP + S_iP.

 

Hierbei gelte

            S_DP = ( f_DP1; f_DP2; f_DP3; ..., F_DPK)         direktes Prägungssignal

                                                                                                                      n Komponenten

            S_DR = ( f_DR1; f_DR2; f_DR3; ...; f_DRL)         direktes Restsignal

            S_iP = ( f_iP1; f_iP2; f_iP3; ... ; f_iPm)              indirektes Prägungssignal

                                                                                                                      m Komponenten

            S_iR = ( f_iR1; f_iR2; f_iR3; ... ; f_iRn)             indirektes Restsignal.

Jede Signalkomponente aktiviert nun circa w = 400 Parallelfasern, die ihrerseits die Purkinjezelle erregen.

Dabei besitzt die synaptische Kopplung für das Prägungssignal den Kopplungswert k = ½, da durch die Kletterfasereinwirkung die Langzeitdepression wirksam geworden ist. Für die Restsignalkomponenten bleibt der Kopplungswert auf dem Wert 1 bestehen, da das Restsignal zu schwach oder zu kurz ist, um eine Langzeitdepression zu erreichen.

Für die gesuchte Feuerrate ohne Korb- und Sternzelleinwirkung gilt:

            f_PZ,G+ = w _* ( ½ _* f_DP1 +  ½ _* f_DP2 +  ½ _* f_DP3 + ... +  ½ _* f_DK +

                        + f_DR1 +  f_DR2 + f_DR3 +  ... + f_DRL

                        + ½ _* f_iP1 + ½ _* f_iP2  + ½ _* f_iP3 +  ... ½ _* f_iPm

 

                               + f_iR1 + f_iR2 + f_iR3 + ...  + f_iRn ) / [ w _* ( m + n)]

Der Faktor w= 400, der der Anzahl der Parallelfasern pro Moosfaser entspricht, kürzt sich auch hier wieder heraus. Es bleibt daher

            f_PZ,G+ = ( ½ _* f_DP1 +  ½ _* f_DP2 +  ½ _* f_DP3 + ... +  ½ _* f_DK +

                        + f_DR1 + f_DR2 + f_DR3 +  ... + f_DRL

 

                        + ½ _* f_iP1 + ½ _* f_iP2 + ½ _* f_iP3 +  ... ½ _* f_iPm

 

                               + f_iR1 + f_iR2 + f_iR3 + ...  + f_iRn ) / [ ( m + n)].

 

            f_PZ,G+ = ( ½ _* f_DP1 +  ½ _* f_DP2 +  ½ _* f_DP3 + ... +  ½ _* f_DK +

 

                        + ½ _* f_DR1 + ½ _* f_DR2 + ½ _* f_DR3 +  ... + ½ _* f_DRL

 

                        + ½ _* f_iP1 + ½ _* f_iP2  + ½ _* f_iP3 +  ... ½ _* f_iPm

 

                               + ½ _* f_iR1 + ½ _* f_iR2 + ½ _* f_iR3 + ...  + ½ _* f_iRn ) / [ ( m + n)]

                        + ( ½ _* f_DR1 + ½ _* f_DR2 + ½ _* f_DR3 +  ... + ½ _* f_DRL

                        + ½ _* f_iR1 + ½ _* f_iR2 + ½ _* f_iR3 + ...  + ½ _* f_iRn ) / [ ( m + n)]

Die ersten vier Zeilen stellen die halbe Feuerrate des Gesamtinputs f dar, die restlichen zwei Zeilen stellen die halbe Feuerrate des Restsignalvektors dar:

            f_PZ,G+ = ½ _* f  + ½ _* f_R.               (Feuerrate der geprägten Purkinjezelle ohne

Hemmung durch Korb- und Sternzelle)

 

Nunmehr müssen wir von dieser Feuerrate diejenige der geprägten Korbzelle f_KO,G und der geprägten Sternzelle f_SZ,G subtrahieren.

Wir erinnern uns        

            f_KO,G = ½ f_D + ½ f_DP               (Feuerrate der geprägten Korbzelle)

            f_SZ,G = ½ f_i + ½ f_iP                  (Feuerrate der geprägten Sternzelle           )

           

Wir subtrahieren diese Feuerraten von derjenigen der geprägten Purkinjezelle und erhalten die resultierende Gesamterregung der Purkinjezelle:

            f_PZ,G+ = ½ _* f  + ½ _* f_R – (½ f_D + ½ f_DP ) – (½ f_i + ½ f_iP )

            f_PZ,G+ = ½ _* f  + ½ _* f_R – ½ f_D - ½ f_DP  – ½ f_i - ½ f_iP )

                                       

            f_PZ,G+ = ½ _* f - (½ f_D + ½ f_i ) – ( ½ f_DP + ½ f_iP ) + ½ _* f_R

 

                f_PZ,G+ = ½ _* f - ½ f  –  ½ f_P + ½ _* f_R

               

                f_PZ,G+ = + ½ f_R –  ½ f_P             (Gesamtfeuerrate der geprägten Purkinjezelle)

Wir erinnern uns daran, dass die Feuerrate selbst nicht negativ werden kann. Wenn in der obigen Differenz der Subtrahend ½ f_P größer ist als der Minuend ½ f_R, dann wir nicht etwa die Feuerrate der Purkinjezelle negativ, sondern die durch die Parallelfasern zugeführte Erregung ist kleiner als die von Korb- und Sternzelle bewirkte Hemmung, so dass also die Hemmung überwiegt. In diesem Falle ist die Purkinjezelle endgültig gehemmt und feuert gar nicht mehr. Daher gilt:

            f_PZ,G+ = + ½ f_R –  ½ f_P wenn f_R = f_P

            f_PZ,G+ = 0 wenn f_R < f_P.

Unter Verwendung der Haviside-Funktion d(x) mit d(x) = x für x = 0 und d(x) = 0 für x < 0 gilt

            f_PZ,G+ = d(+ ½ f_R –  ½ f_P).       (Gesamtfeuerrate der geprägten Purkinjezelle)

Wir bedenken, dass f_R die mittlere Signalintensität des Restsignals und f_P die mittlere Signalintensität des Prägungssignals war. Durch die Prägung wird das Prägungssignal des Cortex zum Eigensignal der Purkinjezelle. Der entsprechende Restsignalanteil wird für diese Purkinjezelle zum Fremdsignalanteil. Ist für eine beliebige Signalkombination S der Eigensignalanteil der Purkinjezelle größer als der Fremdsignalanteil oder ihm gleich, so stellt die Purkinjezelle die bisherige Hemmung des zugehörigen positiven bzw. negativen Kernneurons völlig ein. Als Entdecker dieses Verhaltens, welches vor allem durch das Zusammenwirken der Langzeitdepression in der Purkinjezelle und die gleichzeitige Langzeitpotenzierung in der zugehörigen Korbzelle bzw. Sternzelle hervorgerufen wird, beansprucht der Autor, diesem Phänomen einen selbstgewählten Namen zu geben. Da dieses Verhalten die Grundlage für die Arbeit des Cerebellums als Assoziativspeicher darstellt und die Theorie der Assoziativspeicher bereits im vorigen Jahrhundert von Prof. Günther Palm auf das Gehirn angewendet wurde, soll dieses Theorem auf Vorschlag des Autors als das Theorem von Palm bezeichnet werden.

 

Theorem 1.40: Theorem von Palm: Hemmungswegfall einer Purkinjezelle

                                                           

Die Hemmung des Outputneurons eines Kleinhirnkerns durch die zugehörige Purkinjezelle entfällt immer genau dann, wenn der Eigensignalanteil des vom Cortexclusters eintreffenden nichttrivialen Signals im Mittelwert mindestens so stark ist wie der restliche Fremdsignalanteil.

 

Die Voraussetzung, das Cortexsignal möge nichttrivial sein, ist vonnöten, weil Nullsignale ebenfalls zum Fortfall der Hemmung führen (z. B. Tod).

 

Obiges Theorem überraschte in seiner Aussage selbst den Autor dieser Monografie, hatte er doch jahrelang gehofft, jede Purkinjezelle möge wie die Speicherzelle eines RAM-Speichers nur dann mit einem Signal antworten, wenn ihr Input das Eigensignal wäre.

Da nun aber ein Fremdsignalanteil zulässig ist, der maximal genauso stark sein darf wie der Eigensignalanteil, ist das Cerebellum kein einfacher digitaler Speicher, sondern ein digitaler Suchspeicher. Der Input beim Suchspeicher kann als Frage aufgefasst werden. Im Allgemeinen gibt der Suchspeicher auf eine Frage mehrere Antworten, die als binäres Signal dargestellt wenigstens zur Hälfte mit dem Input übereinstimmen. Doch dazu später.

 

Wir werden nun den Output der positiven bzw. der negativen Kernneuronen in den Kleinhirnkernen berechnen. Hierbei ist von der Normalerregung der Kernneuronen jeweils die hemmende Feuerrate der zugehörigen Purkinjezellen zu subtrahieren. Gezeigt wurde in Theorem 1.35:

 

       f_KN,u = ½ f                               (Feuerrate des ungeprägten Kernneurons),

            f_KN,g = ½ f + ½ f_P                    (Feuerrate des geprägten Kernneurons).

Weiterhin wurde gezeigt:

 

            f_PZ,U = ½ f                               (Feuerrate der ungeprägten Purkinjezelle)

            f_PZ,G+ = d(+ ½ f_R –  ½ f_P).       (Gesamtfeuerrate der geprägten Purkinjezelle)

Daraus berechnen wir die Feuerrate des ungeprägten und des geprägten Kernneurons, welches zu dieser Purkinjezelle gehört, und erhalten:

f_KN,PZ,u = 0                                                      (Gesamtfeuerrate des ungeprägten Kernneurons)

f_KN,PZ,G = ½ f + ½ f_P - d(+ ½ f_R –  ½ f_P).        (Gesamtfeuerrate des geprägten Kernneurons)

Bemerkenswert sind beide Ergebnisse. Das ungeprägte Kernneuron, egal ob glutamaterg oder GABAerg, besitzt gar keine Feuerrate mehr. Es schweigt. Es hat die Feuerrate Null und sein Output ist das Nullsignal.

In der Praxis werden wir bei diesen Kernneuronen allerdings eine schwache Spontanaktivität feststellen, die aber im Mittelwert als „Rauschen“ zu interpretieren sein wird.

Bemerkenswert ist aber auch das Ergebnis für die geprägten Kernneuronen. Hier muss geprüft werden, ob der Eigensignalanteil der Purkinjezelle mindestens so groß ist wie der Restsignalanteil.

Für die geprägten Kernneuronen erinnern wir uns an die Gleichung

            f = f_P + f_R, also auch ½ f_R = ½ f – ½ f_P.

Eingesetzt in

            f_KN,G = ½ f_P + ½ f_R + ½ f_P - d(+ ½ f_R –  ½ f_P) = f_P + ½ f_R - d(+ ½ f_R –  ½ f_P)

folgt

            f_KN,G = f_P + ½ f_R         für f_P = f_R

            f_KN,G = f_P + ½ f_P          für f_P < f_R

Ist f_P = f_R, so ist das Minimum von f_P und f_R gleich f_R.

Wenn jedoch f_P < f_R gilt, so ist das Minimum beider Zahlen gleich f_P.

Daher können wir auch schreiben:

f_KN,G = f_P +  ½ _* min( f_R; f_P )              (Output des geprägten Kernneurons mit Berücksichtigung der Hemmung durch die Purkinjezelle und ohne Kletterfasereinwirkung)

Nunmehr können wir die Feuerraten der verschiedenen Neuronen des cerebellaren Systems sowohl für den ungeprägten als auch für den geprägten Zustand in einer Übersicht zusammenfassen. Wir bezeichnen diese Zusammenfassung als Prägungstheorem des Cerebellums. Hingewiesen sei hier nochmals darauf, dass wir vereinfachend eine Linearität angenommen hatten, also hier eine vereinfachte Variante entstanden ist.

Nicht eingegangen wird auf die unterschiedliche Bedeutung des direkten und des indirekten Cortexsignals. Sollte die Zeit reichen, wird später gezeigt werden, dass das indirekte Signal der Regelung der Empfindlichkeitsschwelle der Assoziativspeicher dient. In relativer Ruhe (bei großer Konzentration) wird das indirekte Signal des aufsteigenden retikulären Aktivierungssystems so schwach, dass die Assoziativmatrix von Fragemodus in den Speichermodus umschaltet.

Weil sich der konstante Anteil ½ f in der Erregung der Kernneuronen auf Grund der rezeptiven Nachbarhemmung durch die glycinergen Interneuronen im den Kleinhirnkernen aufhebt, bleibt am Ende nur die effektive Erregung f_KN,eff  der Kernneuronen übrig.

Theorem 1.41: Prägungstheorem des Cerebellums

Die Feuerraten der ungeprägten und der geprägten Cerebellumneuronen genügt unter der Voraussetzung der Linearität folgenden Gleichungen, wobei f die Feuerrate des Inputsignals ist und sich aus direktem und indirektem Signal zusammensetzt gemäß

f = f_D + f_i.

Weiterhin sei f_P der Anteil des Signalvektors, der prägungswirksam geworden ist, während f_R die Restsignalstärke darstellt gemäß

f = f_P + f_R = f_D,P + f_D,R + f_i,P + f_i,R.

Zellart	Feuerrate ungeprägte Zelle	Feuerrate geprägte Zelle	Bemerkung
Kernneuron (pos. und negativ)	fKN,U- = ½ f	fKN,G- = ½ f + ½ fP	ohne Purkinjeeinwirkung
Korbzelle	fKO,U = ½ fD	fKO,G = ½ fD + ½ fD,P	direktes Signal
Sternzelle	fSZ,U = ½ fi	fSZ,G = ½ fi + ½ fi,P	indirektes Signal
Golgizelle	fGO,U = ½ fD	fGO,G = ½ fD + ½ fD,P	direktes Signal
Purkinjezelle	fPZ,U = ½ f	fPZ,G = 0	für fR < fP
Purkinjezelle		fPZ,G = ½ fR – ½ fP	für fR = fP
Kernneuron/ Purkinjezelle (pos. und negativ)	fKN,PZ,U = 0	fKN,PZ,G = ½ f + ½ fP - d(½ fR – ½ fP)	mit Purkinjeeinwirkung, ohne rezeptive Nachbarhemmung
Kernneuron/ Purkinjezelle/ glycinerge Interneuronen		fKN,eff = d(fP – ½ max(fR, fP))	Der konstante Anteil ½ f hebt sich gegenseitig auf

Ende Theorem 1.41

In allen Angaben wurde die mögliche Einwirkung des Kletterfasersignals vernachlässigt. Der Grund liegt darin, dass das Kletterfasersignal nur während des Prägungsvorganges aktiv ist, nach der Prägung jedoch immer dann vom negativen Kernneuron unterdrückt wird, wenn das Prägungssignal wieder bei der gleichen Zelle auftritt.

Der cerebellare Speicher unterscheidet sich gravierend von einem digitalen Speicher in gewöhnlichen Computern. Ebenso verbirgt sich in seiner Arbeitsweise eine andere Philosophie. Der digitale Speicher im Computer ist sequentiell organisiert und kann nur sequentiell beschrieben und sequentiell abgefragt werden. Sucht man z. B. in einem solchen Speicher das Wort „Auto“, so muss man jede einzelne Speicherzelle auslesen und mit dem Suchwort „Auto“ vergleichen. Als Ergebnis des Suchvorganges erhält man die Adresse der Speicherzelle, in der das Wort „Auto“ gespeichert ist. Analoges gilt, wenn man in der Tabelle einer Datenbank ermitteln will, welcher Kunde mit dem Namen „Maier“ als Reporter arbeitet und in der Stand Elsterwerda wohnt. Hier werden die Tabellenelemente nacheinander abgefragt und mit den Suchwerten verglichen, bis eine Übereinstimmung vorliegt.

Das Cerebellum ist, wie bereits angedeutet, ein Suchspeicher. Es kann auch die Speicherzelle – genauer die Purkinjegruppe – ermitteln, in der ein bestimmtes Eigensignal abgespeichert wurde. Aber der Suchvorgang erfolgt hier nicht sequentiell. Die einzelnen Purkinjegruppen werden nicht zeitlich nacheinander abgefragt, sondern alle auf einmal in einem Ritt.

Während das gesuchte Signal – z. B. das Wort „Auto“ – über die Brückenkerne zu den Moosfasern gelangt, wird es quasi gleichzeitig auf alle Körnerzellen des zugehörigen Cerebellumclusters verteilt. Wegen der enormen Ausbreitungsgeschwindigkeit der Aktionspotentiale entlang der Moosfasern erreicht das Suchsignal alle Körnerzellen fast gleichzeitig. Daher beginnen auch alle Purkinjegruppen gleichzeitig mit der Signalauswertung. Innerhalb von wenigen hundertstel Sekunden entscheidet jede Purkinjegruppe darüber, zu wie viel Prozent das Suchsignal – also der Input – mit ihrem Eigensignal übereinstimmt. Je stärker die Übereinstimmung ist, umso aktiver sind die Eigensignaldetektoren der betreffenden Purkinjegruppe. Dies sind die Korb- und Sternzellen, aber auch die Kernneuronen sowie die Golgizellen.

Gleichzeitig wird geprüft, zu wie viel Prozent das Inputsignal zum Fremdsignal der betreffenden Purkinjegruppe gehört. Je mehr Fremdsignalanteil im Input vorliegt, umso stärker werden die Fremdsignaldetektoren (also die Purkinjezellen) erregt.

Die Eigensignaldetektoren hemmen die Fremdsignaldetektoren, so dass es zu einem Vergleich der Signalstärke von Eigensignalanteilen und Fremdsignalanteilen kommt. Das Resultat ist die Erregung der Kernneuronen, die umso stärker ist, je stärker der Eigensignalanteil war, und die mit wachsender Fremdsignalstärke abnimmt.

Alle Purkinjegruppen, deren Eigensignal die Fremdsignalstärke erreichte oder übertraf, liefern über die Kernneuronen einen Output, wobei auch ohne Signal eine Grunderregung von ½ f, also der halben Inputstärke, vorhanden ist.

Diese Grunderregung wird eliminiert durch die in den Kleinhirnkernen zahlreich vorhandenen hemmenden Interneuronen mit dem Transmitter Glycin. Dennoch bleiben oft mehrere, manchmal sogar viele Kernneuronen aktiv. Dies liegt am Prinzip des Suchgitters. Die Frage „Welche Wörter beginnen mit dem Buchtstaben a“ liefert im Cerebellum innerhalb von wenigen Millisekunden viele tausend Antworten, von denen sich jedoch nur die stärksten durchsetzen. Das Prinzip, wie diese Antworten zwischengespeichert werden, um später nacheinander benannt zu werden, soll hier nicht vorgestellt werden. Hier sei auf Teil 3 und 4 dieser Monografie verwiesen. Wichtig ist die prinzipielle Erkenntnis, dass im Cerebellum die Antworten nicht sequentiell gesucht werden, sondern in einem Prozess geliefert werden, den man als Multitasking bezeichnen kann: Alle Purkinjegruppen eines Cerebellumclusters arbeiten gleichzeitig und parallel zueinander. Und genau diese parallele Arbeitsweise wird ja bei herkömmlichen Computern als Multitasking bezeichnet.

Neben der Fähigkeit zum Multitasking der vielen Purkinjegruppen bildet die Fähigkeit, mehrere oder viele Antworten zu einer Suchanfrage zu liefern, einen weiteren Unterschied zum digitalen Suchspeicher.

Die Arbeit des Cerebellums als Suchspeicher lässt sich nur aus statistischer Sicht wissenschaftlich erklären. Ist S ein Suchsignal, welches wir als Input über die Moosfasern in das Cerebellum einspeisen, so gehört zu diesem Signal eine digitale Signatur. Dazu werden die Elementarsignale wohlgeordnet und ihre Feuerraten auf Binärwerte abgebildet, wobei stärkere Feuerraten den Binärwert 1 erhalten, die schwachen den Binärwert Null. Diese Dualzahl stellt den Suchinput dar.

Die Aufgabe an das Cerebellum lautet nun: Ermittle alle bereits gespeicherten Signale, die dem Input hinreichend ähnlich sind. Denn je mehr aktive Moosfasern des Inputsignals gerade die Eigensignaldetektoren erregen, umso stärker wird der Output der zugehörigen Kernneuronen. Und je mehr aktive Moosfasern die Fremdsignaldetektoren speisen, umso schwächer wird der Output der betreffenden Kernneuronen. Das Cerebellum als Suchspeicher macht also eine statistische Aussage über die Signalähnlichkeit von Input und gespeicherten Cerebellumsignalen. Grundlage der Signalähnlichkeit sind die mit 1 belegten Bit-Positionen in der digitalen Signatur von Input und Output. Je mehr davon an gleicher Position übereinstimmen, umso ähnlicher sind sich zwei Signale.

Zusätzlich besitzt das Cerebellum die erstaunliche Fähigkeit, ein Signal, zu dem es keine hinreichend ähnlichen Signale gibt – welches also noch nicht abgespeichert wurde – ohne speziellen äußeren Befehl vollautomatisch abzuspeichern (wenn dieses Signal hinreichend stark ist und hinreichend lange andauert). Den dennoch vorhandenen Speicherbefehl – das parvocellulare Kletterfasersignal – erzeugt es selbst aus dem nicht unterdrückten Signalmittelwert des zugehörigen Cortexclusters (mit Hilfe des Striosomensystems). Daher hat die Unterdrückung des Kletterfasersignals im Falle der Signalerkennung ein äußerst wichtiges funktionelles Gegenstück: die Nichtunterdrückung des Kletterfasersignals im Falle der Nichterkennung eines hinreichend aktiven Signals. Und dieser Algorithmus erlaubt eine (unbewiesene) Erweiterung: Wenn starke Signale nicht erkannt werden, wird das Kletterfasersignal nicht unterdrückt. Sollten aber keine freien Purkinjegruppen vorhanden sein (weil sie alle aufgebraucht worden sind), kann das aktive und starke Kletterfasersignal eine der bereits geprägten Purkinjegruppen mit dem neuen Signal prägen – also überschreiben – wenn diese Purkinjegruppe sich nicht „dagegen wehrt“. „Sich dagegen wehren“ bedeutet in diesem Falle, dass diese Purkinjegruppe ihr Signal etwas oder sogar etwas mehr „vergessen“ hat. Sollte eine Purkinjegruppe ihr Signal vergessen, wenn es längere Zeit nicht auftrat, wäre über die dann erfolgende Schwächung der Hemmung des Kletterfasersignals der Weg geebnet für eine „Neuprägung“ oder „Umprägung“ mit einem völlig anderem, aber statistisch häufigerem Signal. Dieser Algorithmus wird in dieser Monografie später erneut aufgegriffen werden.

 

An dieser Stelle sollte auf den bereits mehrfach benutzten Begriff der rezeptiven Nachbarhemmung hingewiesen werden. Wenn das Cerebellum z. B. den Input verarbeitet, der ihm aus den Rezeptoren der Körperoberfläche zugeleitet wird, ist die Inputmenge gewaltig. Analog gibt es eine gewaltige Outputmenge. Es ist daher systemtheoretisch äußerst sinnvoll, den schwächeren Output zu unterdrücken, wodurch der stärkere Output an Kontrast gewinnt. Zur Hemmung reicht es aus, wenn jedes Outputneuron über hemmende Interneuronen die benachbarten Outputneuronen hemmt. Stärker erregte Outputneuronen hätten so eine stärkere Umgebungshemmung zur Folge. Und da diese Hemmung mit wachsendem Abstand abnimmt, sprechen wir von einer rezeptiven Hemmung. Sie hat die Entstehung der rezeptiven Felder in neuronalen Systemen zur Folge.

Im Cerebellum wird die rezeptive Hemmung des Outputs in zwei Stufen bewirkt. Einmal wird direkt in den Cerebellumkernen eine rezeptive Nachbarhemmung über die glycinergen Interneuronen verursacht. Und zweitens erreicht der erregende Cerebellumoutput den Thalamus. Dort befinden sich Unmengen von hemmenden Interneuronen, wodurch wiederum die stärkeren Signale bevorzugt, aber die schwächeren anteilig gehemmt werden. Daher ist die rezeptive Nachbarhemmung im Thalamus eine wesentliche Voraussetzung, um den Cerebellumoutpout überhaupt sinnvoll bewerten zu können. Die rezeptive Nachbarhemmung wird sich noch in vielen anderen Bereichen als äußerst nützlich erweisen.

 

Nunmehr können wir die Prägung des Cerebellums als rekursiven Prozess begreifen, bei dem schrittweise und nacheinander jeweils eine Purkinjegruppe geprägt wird. Hierbei werden alle Purkinjezellen einer Purkinjegruppe mit dem gleichen Signal geprägt. Doch dazu später.

Wir denken uns also ein Prägungssignal S_P, welches gemeinsam mit dem Kletterfasersignal auf das Cerebellum einwirkt. Anfangs sei noch keine einzige Purkinjegruppe geprägt. Das primäre Kletterfasersignal möge vermittels zentraler oder sequentieller Verteilung die sekundären Kletterfasersignale liefern.

Sämtliche Kernneuronen sind ungeprägt und liefern das Nullsignal. Dieses Nullsignal kann das zentrale Verteilungsneuron nicht hemmen, auch bei einer sequentiellen Verteilung tritt nirgendwo eine Hemmung auf.

Daher sind alle sekundären Kletterfasersignale identisch mit dem primären Kletterfasersignal und wirken stark erregend auf alle beteiligten Zellen ein.

Wir beginnen unsere Resultatanalyse bei den Golgizellen. Sie werden alle von den Kletterfasern kontaktiert. Jede Golgizelle am Ende einer jeden Purkinjegruppe wird stark erregt. Sie unterbricht durch ihre stark hemmende Wirkung die Weiterleitung der Moosfasersignale auf den Moosfasern. Nur die Startgruppe, also die erste Purkinjegruppe erhält den aktuellen Moosfaserinput, da die Hemmung durch die Golgizelle am Ende der Startgruppe einsetzt, so dass erst hinter dieser Startgruppe die Moosfasern signallos werden.

Gleichzeitig erhalten die Purkinjezellen, die Korbzellen, die Sternzellen und die Golgizelle der Startgruppe zusätzlich zum Moosfaserinput den stark erregenden tetanischen Kletterfaserinput. Dadurch werden in der Startgruppe der Purkinjegruppen die dort vorhandenen Purkinjezellen geprägt, ebenso die Korbzellen, die Sternzellen und die Golgizellen. Aber die Golgizelle wird gleichzeitig vom starken Kletterfasersignal erregt und hemmt daher die Weiterleitung der Moosfasersignale zu den benachbarten Purkinjegruppen. Daher erhält nur die Startgruppe einen Moosfaserinput. Da dieser zusammen mit dem tetanischen Kletterfaserinput mindestens eine Sekunde einwirkt, werden alle Zellen dieser Startgruppe geprägt. Alle anderen Gruppen können nicht geprägt werden, weil der Moosfaserinput fehlt. Dieser wird durch die Golgizelle der Startgruppe, die sich immer als letzte Zelle dieser Gruppe am Ende befindet, völlig unterdrückt.

Die Signale der sekundären Kletterfasern sind identisch mit dem Signal der primären Kletterfaser, weil sie nur durch Verteilung aus ihm hervorgehen. Aber jedes sekundäre Kletterfasersignal erregt stark und länger andauernd die Golgizelle am Ende der zugehörigen Gruppe, so dass dort ebenfalls eventuell vorhandene Restsignale völlig unterdrückt werden. Dies wäre möglich, wenn die Golgizelle der Startgruppe inzwischen beispielsweise abgestorben wäre. Also kann keine Purkinjegruppe außer der ersten mit dem eintreffenden Prägungssignal geprägt werden.

Nach der Prägung der ersten Purkinjegruppe treffen weitere Signale aus dem Cortex ein. Hier gibt es zwei Möglichkeiten.

Entweder das Signal ist identisch mit dem ersten Prägungssignal. Dann erkennen die Purkinjezellen der Startgruppe ihr Signal wieder. Das zugehörige positive Kernneuron antwortet mit einem starken Output zum Thalamus. Das zugehörige negative Kernneuron unterdrückt mit seinem starken hemmenden Output das zentrale Verteilungsneuron in der Olive bzw. das zugehörige erste Neuron in der sequentiellen Verteilungskette.

Enthält das Inputsignal das Prägungssignal wenigstens zur Hälfte, ist die Reaktion analog. Der Thalamus wird über die Erkennung informiert und das negative Kernneuron unterdrückt die Erzeugung weiterer Kletterfasersignale zu den anderen Purkinjezellen.

Nach der Prägung der Startgruppe (oder einer folgenden Gruppe von Purkinjezellen) stellt sich allerdings die Frage, warum die Purkinjezelle ihr Prägungssignal, welches durch den Vorgang der Prägung zum Eigensignal geworden ist, nicht wieder verliert. Denn nach wie vor werden ja bei der zentralen Verteilung und bei der sequentiellen Verteilung die Purkinjezellen geradezu mit Kletterfasersignalen überschüttet. Jedes stärkere Signal, welches bisher noch nicht abgespeichert wurde und somit nicht erkannt wird, führt zu einem starken Kletterfasersignal. Weil dieses Signal allen bisher geprägten Purkinjegruppen fremd ist, wird jede geprägte Purkinjezelle ihr positives und ihr negatives Kernneuron im Kleinhirnkern stark hemmen. Daher wird kein negatives Kernneuron aktiv sein, welches das Kletterfasersignal unterdrücken könnte. Warum wird nun eine bereits mit einem anderen Signal geprägte Purkinjezelle (oder Gruppe) nicht vom alten auf das neue Cortexsignal „umgeprägt“? Schließlich ist ihr Kletterfasersignal aktiv, wenn sie ihr eigenes Eigensignal nicht wiedererkennt, aber auch keine andere Purkinjegruppe genau dieses Signal als ihr Eigensignal erkennt.

Die Lösung dieses offenen Problems beschäftigte den Verfasser dieser Monografie mehrere Jahre. Hierbei galt es, die verfügbaren Fakten zu sichten, denn nur die Natur konnte eine Lösung gefunden haben. Die Antwort auf die offene Frage, warum eine bereits geprägte Purkinjezellen während der Aktivität eines bisher unbekannten Signals durch das zugehörige Kletterfasersignal nicht umgeprägt wird, soll in einem neuen Theorem beantwortet werden. Der Autor nimmt sich die Freiheit, dieses Theorem nach der Hauptstadt seines Geburtslandes Polen als das Warschauer Theorem zu bezeichnen.

Theorem 1.42: Warschauer Theorem

Das ersterregte Neuron hemmt die später erregten.

Seine besondere Bedeutung erhält das Warschauer Theorem bei der Digitalisierung von analogen neuronalen Daten. Aber bereits beim Cerebellum ist seine Bedeutung immens. Dies werde nachfolgend begründet.

Wenn ein Neuron – beispielsweise das negative Kernneuron im Cerebellumkern – gleichzeitig oder mit geringem Zeitabstand sowohl erregt als auch gehemmt wird, so ist die resultierende Erregung deutlich geringer als erwartet. Oft bleibt von der zugeführten Erregung gar nichts übrig, weil die Hemmung völlig überwiegt. Insbesondere wenn die hemmenden Axone günstig – also in der Nähe des Axonhügels – platziert sind.

An dieser Stelle soll nochmals das Werk „Das Gehirn“ von Richard F. Thompson vom Spektrum Akademischer Verlag würdigend zitiert werden. Auf Seite 93 der 3. Auflage lesen wir die leichtverständliche Erklärung:

(Zitatbeginn:)

Wechselwirkung zwischen Erregung und Hemmung

Das inhibitorische postsynaptische Potenzial hat eine stärkere Wirkung als das exzitatorische. Wenn eine inhibitorische Synapse aktiv ist, sorgt sie gewissermaßen für einen Kurzschluss. Die erhöhte positive Ladung an der exzitatorischen Synapse kann dort abfließen, und die Membran am Axonhügel wird folglich viel weniger depolarisiert.

                                                                                                                      (Zitatende)

Dem zitierten Text ist eine überaus leichtverständliche Abbildung vorangestellt, die den Sachverhalt erklärt.

Wenn nun die hemmende Wirkung die zeitlich erste ist, während die erregende Wirkung erst später einsetzt, so ist das Endergebnis vorhersehbar: das Neuron wird gehemmt bleiben.

Wie ist dies beim Cerebellum anwendbar?

Bekanntlich treffen die Moosfasersignale aus dem Cortex deutlich früher im Cerebellum ein als das vom Mittelwert abgeleitete Kletterfasersignal. Denn der Weg des Mittelwertsignals der Aktivitätsneuronen führt über die Substantia nigra pars compacta, von dort zur Matrix des Striatums, weiter zum Globus pallidus interna, weiter zum Nucleus ruber und über die Olive zum Cerebellum. Daher trifft ein Kletterfasersignal mit deutlicher Verspätung im Cerebellum ein. In dieser Zeitdifferenz sind die Cortexsignale über die Brückenkerne längst im Cerebellum angekommen. Und jede Purkinjezelle, die ihr Eigensignal nicht erkannte, hatte Zeit genug, eine starke hemmende Erregung aufzubauen.

Die stark hemmende Erregung wird über Kollateralen innerhalb der gleichen Purkinjegruppe weitergereicht an die angeschlossenen Korbzellen, Sternzellen und an die Golgizelle.

Korbzelle, Sternzelle und Golgizelle sind also sehr stark gehemmt und können von einem eventuell eintreffenden Kletterfasersignal nicht mehr geprägt werden, denn die dort mögliche Langzeitpotenzierung benötigt eine erregte Zelle. Bei einer stark gehemmten Zelle wird keinerlei LTP auftreten.

Da die Golgizelle am Gruppenende stark gehemmt ist, wird von ihr keinerlei Weiterleitungshemmung bewirkt. Die eintreffenden Moosfasersignale können sich also ungehindert zu den Nachbargruppen ausbreiten.

Zu diskutieren wäre, ob das Kletterfasersignal eine gewisse Wirkung auf die stark erregte Purkinjezelle haben könnte, so dass es eventuell zu einer Langzeitdepression zwischen gerade aktiven Parallelfasern und der Purkinjezelle kommen würde. In diesem Falle wäre die Purkinjezelle ein Fremdsignaldetektor sowohl für das erste geprägte Signal als auch für das zweite, dritte, vierte Prägungssignal der Nachbargruppen. Nach sehr vielen Prägungen verschiedenster Signale würde die Purkinjezelle auf jedes von ihnen mit um die Hälfte verminderter Erregung reagieren. Dies würde aber die Funktion der Korb- und Sternzellen sowie der Golgizellen als Eigensignaldetektoren nicht beeinträchtigen. Denn diese werden mit Sicherheit nicht umgeprägt, da die stark hemmende Purkinjezelle eine weitere LTP wirksam verhindert. Wenn nun mit einer gewissen Zeitverzögerung das Kletterfasersignal versucht, die positiven oder negativen Kernneuronen zu erregen, laufen diese Bemühungen ins Leere. Der stark hemmende Einfluss der Purkinjezelle – die ihr Eigensignal ja nicht erkannt hatte – verhindert durch den synaptischen „Kurzschluss“ eine Erregungswirkung.

Insofern hemmt das ersterregte Neuron, hier also die Purkinjezelle, die später erregten Neuronen, mit denen es synaptisch verbunden ist. Deshalb hemmt die stark erregte Purkinjezelle, wenn sie ihr Eigensignal nicht wiedererkennt, sowohl die zugehörige Korbzelle, die zugehörige Sternzelle, aber auch die Golgizelle am Ende der Gruppe sowie ebenso die Kernneuronen im Cerebellumkern.

Die Kernneuronen liefern daher keinerlei Output, wenn eine geprägte Purkinjezelle ihr Eigensignal nicht erkennt und wenige Zeit später ein starkes Kletterfasersignal diese Neuronen zu erregen versucht. Letztlich ist die synaptische Kopplung des Kletterfasersignals zu den Kernneuronen nicht so stark wie die synaptische Kopplung mit der Purkinjezelle.

Bisher haben wir folgendes erklärt:

-          Die Purkinjezellen der Startgruppe werden als erste mit dem ersten Prägungssignal aus dem Cortexcluster geprägt.

-          Während der Prägung verhindert die Golgizelle dieser Startgruppe die Weiterleitung der Moosfasersignale zu den Nachbargruppen, wodurch deren gleichzeitige Prägung mit dem gleichen Signal verhindert wird. Die Erregung der Golgizellen der folgenden benachbarten Purkinjegruppen durch das Kletterfasersignal hat die gleiche Wirkung.

-          Trifft ein neues, anderes Signal aus dem Cortex ein, dem danach das zugehörige Kletterfasersignal folgt, so wird eine Umprägung der Korb-, Stern- und Golgizellen der Startgruppe wirksam verhindert, weil sie von der aktiven Purkinjezelle gehemmt werden.

-          Eine Umprägung der Purkinjezelle als Fremdsignaldetektoren ist theoretisch möglich.

-          Der Output der Kernneuronen der Startgruppe während der Prägung anderer Purkinjegruppen mit anderen Prägungssignalen ist das Nullsignal, da die hemmende Wirkung der Purkinjezellen der Startgruppe einer Erregung durch das Kletterfasersignal zuvorkommt und diese Erregung durch Kurzschließen annulliert.

Nunmehr müssen wir zeigen, wie die übrigen Purkinjegruppen mit weiteren, anderen Prägungssignalen geprägt werden. Die Prägung der ersten Gruppe wurde aufgezeigt. Wir zeigen, wie die k-te Purkinjegruppe geprägt wird, wenn alle ihre Vorgängergruppen bereits mit je einem eigenen Prägungssignal geprägt worden sind. Gelingt dies, so haben wir im Sinne der vollständigen Induktion gezeigt, dass alle Purkinjegruppen der Reihe nach jede mit einem anderen Prägungssignal geprägt worden sind. Genau dies versuchen wir nun.

Aus dem Cortex möge über die Brückenkerne und die Moosfasern ein Signal in das zugehörige Cerebellumcluster einströmen, welches nicht das Prägungssignal der ersten (k-1) Purkinjegruppen sein soll.

-          Keine der ersten k-1 Purkinjegruppen erkennt dieses Signal als ihr Eigensignal wieder.

-          Jede Purkinjezelle der Gruppen 1 bis k-1 ist daher stark erregt. Sie hemmt die Golgizelle am jeweiligen Gruppenende, so dass es zu keiner Weiterleitungshemmung der Moosfasersignale kommen kann.

-          Daher erhalten die Zellen der k-ten Purkinjegruppe das komplette Cortexsignal als Input.

-          Gleichzeitig erhalten alle Purkinjezellen ein Kletterfasersignal, wenn das primäre Kletterfasersignal mit Hilfe der zentralen oder sequentiellen Verteilung auf alle übrigen sekundären Kletterfasern verteilt wird.

-          Keine der ersten k-1 Purkinjegruppen hemmt dieses Kletterfasersignal an der Verteilungsstelle, weil keine der zugehörigen Purkinjegruppen ihr Prägungssignal erkennt.

-          Das Kletterfasersignal bewirkt in der k-ten Purkinjegruppe die starke Erregung der Golgizelle, so dass diese die Signalweiterleitung auf den Moosfasern zu den Nachbargruppen verhindert. Dadurch kann keine Purkinjegruppe nach dieser k-ten Gruppe Moosfasersignale empfangen. Daher findet hinter der k-ten Gruppe keine Prägung mit dem aktuellen Prägungssignal statt, weil zwar die tetanische Erregung durch das Kletterfasersignal vorhanden ist, aber die meisten Parallelfasern signallos bleiben. Bedacht werden muss hier allerdings, dass die Golgizellen auf Grund der Prägung durch das Kletterfasersignal eine Langzeitpotenzierung erleiden. Daher ist ihre synaptische Kopplung zu den Eigensignalanteilen doppelt so stark wie zu den Fremdsignalanteilen. Daher werden Fremdsignale nicht so gut unterdrückt und können sich sehr wohl, wenn auch geschwächt, zur Nachbar-Purkinjegruppe hindurcharbeiten. Da vor der betrachteten k-ten Purkinjegruppe bereits k-1 Purkinjegruppen liegen, in denen pro Purkinjegruppe eine neue Körnerzelle ein neues Parallelfaseraxon bildet, verfügt die k-te Gruppe pro Moosfaser bereits über k Parallelfasern der gleichen Moosfaser. Wenn diese Moosfaser einem Fremdsignalanteil zugeordnet ist, hemmt zwar jede Golgizelle dieses Signal, aber nur halb so stark wie die Eigensignale. Durch die Vervielfachung über die sequentielle Verteilungskette der Parallelfasern können also Fremdsignale in der Summe noch relativ stark werden. Daher kann eine Purkinjezelle, die ein Eigensignal erkennt, die Prägung der benachbarten, freien Purkinjegruppe mit einem völlig anderem Prägungssignal, welches gleichzeitig vom Cortex über die Brückenkerne einströmt, nicht verhindern. Verhindert wird nur die Prägung des gleichen Signals in den Nachbargruppen!

-          In der k-ten Purkinjegruppe bewirkt die starke tetanische Erregung durch die Kletterfaser und die gleichzeitige Erregung durch das Prägungssignal die Prägung der beteiligten Zellen: die Purkinjezellen, die Sternzellen, die Korbzellen, die Golgizelle sowie das positive und negative Kernneuron werden mit dem k-ten Prägungssignal geprägt. Dadurch werden die Purkinjezellen zu Fremdsignaldetektoren, während die übrigen Zellen zu Eigensignaldetektoren werden.

-          In der k-ten Purkinjegruppe wird die Golgizelle am Ende dieser Gruppe ebenfalls vom eintreffenden Kletterfasersignal sehr stark erregt, wodurch sie eine doppelte Weiterleitungshemmung verursacht. Sie unterbricht die Weiterleitung des Moosfaserinputs zu den auf sie folgenden Purkinjegruppen ebenso wie die Weiterleitung der Moosfasererregung zu den von ihr erreichbaren Körnerzellen. Wegen des Fehlens der Moosfasersignale können also alle nach der k-ten Purkinjegruppe angeordneten Purkinjegruppen nicht durch die eintreffenden Kletterfasersignale geprägt werden, da die Parallelfasersignale fehlen.

-          Ist jedoch der Prägungsvorgang der k-ten Purkinjegruppe komplett vollzogen und das gleiche Signal wirkt unverändert weiter über die Moosfasern ein, so erkennt die k-te Purkinjegruppe dieses Signal nunmehr als Eigensignal. Das positive Kernneuron der k-ten Gruppe meldet die Signalerkennung dem Thalamus. Das negative Kernneuron hemmt sofort das Kletterfasersignal und verhindert, dass irgendeine Purkinjegruppe mit diesem Signal geprägt werden könnte.

-          Trifft aus dem Cortex ein Signal ein, dass von keiner der k bereits geprägten Purkinjegruppen als Eigensignal erkannt wird, so hemmt jede der ersten k Purkinjegruppen die Golgizelle am Ende der Gruppe. Dadurch fällt die Golgihemmung weg, die Moosfasersignale erreichen die (k+1)-te Gruppe, die noch ungeprägt ist. Da kein Kletterfasersignal gehemmt wird, wird die (k+1)-te Gruppe mit diesem neuen Signal geprägt, falls es prägungsfähig, also hinreichend stark und hinreichend lang andauernd ist.

Die grundlegende Funktionsweise der Neuronen im Cerebellum beruht auf der Spezialisierung der Neuronen in Zuge der Prägung durch den tetanischen Kletterfaserinput und das gleichzeitige Einwirken der Prägungssignale. Durch Langzeitpotenzierung werden die Korbzellen, die Sternzellen, die Golgizellen, die positiven sowie die negativen Kernneuronen zu Eigensignaldetektoren. Ihr Output auf ein Eigensignal ist deutlich stärker als auf ein Fremdsignal. Auch auf eine vektorielle Mischung von Eigensignalanteil und Fremdsignalanteil reagieren sie als Eigensignaldetektoren.

Die Purkinjezellen dagegen reagieren nach dem Prägungsvorgang durch die Langzeitdepression als Fremdsignaldetektoren. Fremdsignalanteile wirken deutlich stärker erregend als Eigensignalanteile. Durch die zusätzliche Hemmung der Purkinjezellen mit dem Output der Eigensignaldetektoren, hier der Korb- und Sternzellen – wird die Purkinjezelle genau dann völlig gehemmt, wenn der Fremdsignalanteil der Purkinjezelle kleiner oder gleich dem Eigensignalanteil der Korb- und Sternzelle ist. In diesem Falle halten sich Fremdsignal und Eigensignal die Waage.

Aus dem Gleichgewicht wird das Ganze gebracht, wenn die Stärke des indirekten Signals gegen Null geht. Durch „stille Einkehr“, durch Konzentration oder das Fehlen störender Reize, also durch eine stressfreie Situation wird das indirekte Cortexsignal aus der Formatio reticularis (ARAS) stark vermindert. Das indirekte Signal war aber beim stressgeplagten Prägungsprozess bereits vorhanden und gehört daher zum großen Teil zum Eigensignal. Wenn nun Stressfreiheit und innere Ruhe den indirekten Eigensignalanteil vermindert, so kommt die Waage aus Eigensignal und Fremdsignal aus dem Gleichgewicht zum Nachteil des Eigensignals. Daher liefert die Assoziativmatrix plötzlich zahlenmäßig weniger „Antworten“. Nicht mehr viele ähnliche Signale liefern einen Erkennungsoutput, sondern nur noch die, die mit dem direkten Cortexsignal stark verwandt sind. Die Antworten werden also präziser. Genau dies ist der Vorgang, der beim Lernen als „inneres Konzentrieren“ bezeichnet wird. Die Frage: „Wer frisst am liebsten Fleisch und Knochen?“ liefert also unter Stress viele Antworten: Hunde, Wölfe, Schakale, Löwen, Tiger... usw. Wird die Frage später in völlig entspannter Atmosphäre wiederholt, ist die Antwort eine ganz andere: „Unser Hund Djego *) frisst am liebsten Fleisch und Knochen!“ Plötzlich gibt es nur noch eine Antwort! Daher hat das aufsteigende retikulare System nicht nur eine große Bedeutung bei der Aktivierung der Cortexrinde (ARAS), sondern auch bei der Regelung des Arbeitspunktes der Assoziativmatrizen des Cerebellums. Der Autor ist der Überzeugung, dass diese Erkenntnis hier in dieser Monografie erstmalig dargestellt wird. Aber auch der dazu inverse Algorithmus ist möglich: die Erhöhung der Empfindlichkeit und Antwortvielfalt durch stärkere indirekte Signale, z. B. durch die Mittelwertsignale des Schmerzsystems.

Wir fassen diese Erkenntnis in ein eigenes Theorem.

*) Djego heisst der Hund der Familie des Autors

Theorem 1.43: Die Funktion des indirekten Cortexsignals im Cerebellum

Das indirekte Cortexsignal entstammt dem aufmerksamkeitssteuernden System und wird im Standardfalle ein Teil des Prägungssignals und damit des Eigensignals der Purkinjegruppen. Nimmt seine Stärke später durch äußere Umstände (Stressfreiheit“) oder innere Vorgänge (Konzentration) ab, so wird in den Assoziativmatrizen des Cerebellums der Arbeitspunkt verschoben.

Die Verschiebung erfolgt vom Fragemodus mit relativ vielen Antworten in den Speichermodus mit relativ wenigen Antworten. Die resultierenden Outputsignale zeichnen sich dadurch aus, dass ihr Fremdsignalanteil geringer ist, weil der Eigensignalanteil des indirekten Signals infolge der besseren Konzentration abgenommen hat. Dadurch verringert sich die Anzahl verschiedener Outputsignale auf ein Inputsignal mit abnehmender Signalstärke des indirekten Signals, die Antwortvielfalt wird also geringer.

Umgekehrt bewirken stärkere indirekte Signale eine Zunahme der Antwortvielfalt und Signalempfindlichkeit des Cerebellums.

Ebenso erzeugt eine plötzliche Zunahme des Fremdsignalanteils, z. B. durch unerwarteten Lärm (Schreie, Donner, Schüsse), starke visuelle Reize (Blitze, schnelle Bewegung großer Objekte, Feuer), zusätzliche olfaktorische Belastung (Rauch) eine gleichartige Verschiebung des Arbeitspunktes vom Fragemodus mit vielen Antworten zum Speichermodus mit wenigen Antworten, da dann nur die Purkinjezellen antworten, deren Eigensignal so stark ist, dass es von den starken Fremdsignalen nicht übertönt wird. Im Extremfalle gibt es gar keinen Cerebellumoutput (auch keinen motorischen!), das betreffende Lebewesen ist dann vor Angst gelähmt und verfällt in die Angststarre. Das „Totstellen“ ist also nicht unbedingt eine aus der Intelligenz geborene Entscheidung, sondern eine Zwangsreaktion auf übermäßig starke Fremdsignalanteile im Moosfaserinput des Cerebellums.

Die speziellen Aufgaben der Eigensignaldetektoren und der Fremdsignaldetektoren in Cerebellum fassen wir in dem nachfolgenden Theorem zusammen.

 

Theorem 1.44.: Die Arbeitsteilung von Eigensignal- und Fremdsignaldetektoren im Cerebellum

Die Eigensignaldetektoren im Cerebellum haben die Aufgabe,

-          die Eigensignalanteile zu erkennen (Korb- und Sternzellen, Golgizellen, Kernneuronen)

-          im Erkennungsfalle die Fremdsignaldetektoren (Purkinjezellen) zu hemmen

-          die Signalerkennung dem Thalamus und somit auch dem Cortex zu melden (positive Kernneuronen)

-          Die Signalweiterleitung der Eigensignalanteile entlang der Moosfasern im Erkennungsfalle zu hemmen (Golgizellen)

-          Die Signalweiterleitung der Eigensignalanteile entlang der erreichbaren Körnerzellaxone zu den Parallelfasern innerhalb der gleichen Purkinjegruppe im Erkennungsfalle zu hemmen (Golgizellen)

-          Bei Erkennung der Eigensignalanteile das zugehörige Kletterfasersignal zu hemmen (negative Kernneuronen hemmen Kletterfaserneuron in Olive)

Die Fremdsignaldetektoren im Cerebellum haben die Aufgabe

-          die Fremdsignalanteile zu erkennen (Purkinjezellen)

-          die mittlere Stärke der Fremdsignalanteile mit der mittleren Stärke der Eigensignalanteile zu vergleichen und durch Differenzbildung zwischen Fremdsignalstärke und Eigensignalstärke das stärkere Signal zu ermitteln (Purkinjezellen, von aktiven Korb- und Sternzellen gehemmt)

-          im Falle, dass die Fremdsignalstärke überwiegt, wird die Weiterleitungshemmung der Golgizellen verhindert, so dass sich die Moosfasersignale ungestört zu den benachbarten Purkinjegruppen ausbreiten können (Purkinjezellen hemmen Golgizellen)

-          im Falle, dass die Fremdsignalstärke überwiegt, werden die als Eigensignaldetektoren wirkenden Korbzellen, Sternzellen und Golgizellen und Kernneuronen von den zugehörigen Fremdsignaldetektoren (den Purkinjezellen) sehr stark gehemmt, um eine mögliche Umprägung durch ein eintreffendes Kletterfasersignal zu verhindern

-          im Falle, dass die Fremdsignalstärke überwiegt, wird der Output des negativen Kernneurons stark gehemmt. Dadurch kann dieses Kernneuron das zugehörige Verteilungsneuron im Nucleus olivaris nicht mehr hemmen. Dessen Output wiederum kann als neues Kletterfasersignal für die benachbarte Purkinjegruppe verwendet werden. Ist diese Gruppe noch ungeprägt, wird sie nun bei hinreichender Signalstärke mit dem anliegenden Signal geprägt.

Nun wird endgültig klar, dass die Neuronen des Cerebellums ein wohlabgestimmtes signalverarbeitendes System darstellen, dessen Aufgabe in der automatischen Speicherung wesentlicher (also prägungsfähiger) Cortexsignale besteht.

Die Gesamtschaltung des Cerebellums am Beispiel zweier Purkinjegruppen, jede bestehend aus drei Purkinjezellen, wird in der nachfolgenden Skizze dargestellt.

Wegen der Kürze der Axone wird der hemmende Output der Korb- und Sternzellen zeitnah wirksam. Beachtet werden sollte, dass die (längeren) hemmenden Axone der Purkinjezellen schnellleitend sein sollte, da die cerebellare Schaltung durchaus ein zeitkritisches Verhalten besitzt.

Skizze 1.25: Die Schaltung des Cerebellums

 

 

 

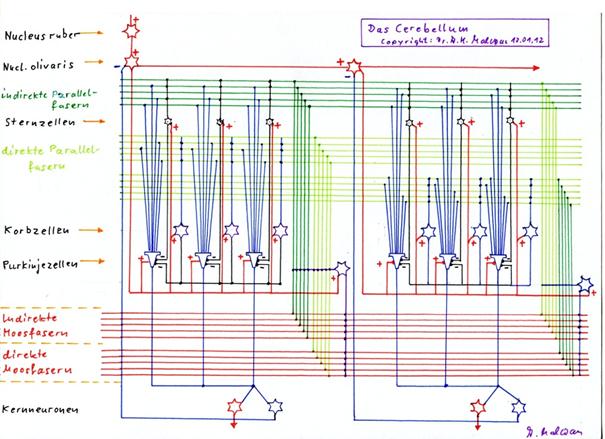
(Die hemmenden Axonkollateralen der Purkinjezellen zu den Korb-, Stern- und Golgizellen wurden aus Gründen der Übersichtlichkeit weggelassen)

 

Für Nichtmathematiker wird es natürlich etwas schwieriger sein, zu verstehen, warum eine Purkinjezelle ein Eigensignal erkennt, obwohl es von einem Fremdsignalanteil überlagert werden kann. Das Cerebellum arbeitet sozusagen als Suchspeicher.

Ein Suchspeicher beantwortet Fragen. Der Input des Suchspeichers ist ein Signalvektor, der als Frage aufgefasst wird. Die Antwort des Suchspeichers liefern die Outputneuronen der Kleinhirnkerne. Sie sind immer genau dann erregt, wenn das Eigensignal der zugehörigen Purkinjezellen wenigstens zur Hälfte mit dem Inputsignal übereinstimmt.

 

Beispiel:

 

Auf den Input „Haus“ liefert ein Suchgitter z. B. die nachfolgenden Begriffe als Output:

 

-          Haustür

-          Hausdach

-          Bauhaus

-          im Haus

-          ...,

 

Kennzeichnend ist, dass der Input aus 4 Buchstaben besteht, der Output dagegen aus maximal 8 Buchstaben. Damit stimmt der Input „Haus“ zu wenigstens 50 % mit dem Output überein, enthält also das Prägungssignal wenigstens zur Hälfte.

Bereits vor Jahrzehnten wurden die vermuteten Zusammenhänge von Inputvektor und Outputvektor der Purkinjezellen (allerdings ohne Berücksichtigung des Korb- und Sternzellanteils!) in einer Matrix zusammengefasst, die als „Assoziativmatrix“ in die Geschichte einging.

An dieser Stelle sei Herrn Professor Günther Palm recht herzlich gedankt für sein Interesse an den Ideen des Autors, weit mehr aber für seine erfolgreichen Bemühungen, den Autor auf die Verbindung des Cerebellums mit der Theorie der Assoziativspeicher hinzuweisen. Erst dadurch wurde dem Autor so richtig verständlich, warum eine Purkinjezelle auf einen Input antwortet, von dem sie quasi nur die „Hälfte“ des Signals abgespeichert hatte. Günther Palm forscht seit Jahrzehnten erfolgreich auf dem Gebiet der Entstehung neuronaler Intelligenz.

Das theoretische Modell des Autors dieser Monografie erweitert seine Theorie der Assoziativspeicher dahingehend, dass nunmehr das Kletterfasersignal als Schreibbefehl auftritt und das Hebbsche Lernen ersetzt, wodurch der Lernprozess für ein einzelnes Signal auf die Zeitdauer von einer Sekunde (Beispielwert) verringert werden kann. Zweitens werden der Assoziativmatrix ständig neue Signale hinzugefügt, also ihre Spaltenanzahl ständig erhöht, bis die Anzahl der ungeprägten Purkinjezellen des Cerebellumclusters aufgebraucht ist und sich keine neuen mehr bilden können. Und letztlich zeigt das Modell des Autors die Herkunft des Cerebelluminputs auf. Besonders erfreulich ist der Nachweis, dass die vielen Millionen Cortexcluster jeder für sich eine eigene Assoziativmatrix im Cerebellum bilden und alle parallel zueinander arbeiten.

 

Wir fassen die prinzipielle Arbeitsweise des Cerebellums als neuronalen Speicher für Komplexsignale unter Verwendung der magnocellularen Kletterfasersignale in ein eigenes Theorem.

 

Theorem 1.45: Das magnocellulare Kletterfasersignal als Speicherbefehl des Cerebellums

Das primäre magnocellulare Kletterfasersignal, welches vom Striosomensystem der Basalganglien aus dem Aktivitätsneuron eines Cortexclusters abgeleitet wird, sowie die aus ihm abgeleiteten übrigen sekundären magnocellularen Kletterfasersignale bilden eine Klasse von neuronalen Schreibbefehlen des Cerebellums. Sie bewirken die zwangsweise Abspeicherung der während ihrer Aktivität an den Parallelfasern anliegenden prägungsfähigen Signale in der nächsten freien Purkinjegruppe. Somit speichert das Cerebellum vermittels dieser Kletterfasersignale die im zugehörigen Cortexcluster auftretenden prägungsfähigen Komplexsignale, wobei jedem prägungsfähigen Komplexsignal eine Purkinjegruppe zugeordnet ist. Tritt ein bereits abgespeichertes Komplexsignal später erneut als Input des Cerebellums auf, so wird es von der Purkinjegruppe erkannt, deren Prägungssignal es war, vorausgesetzt, der Fremdsignalanteil ist nicht stärker als der Eigensignalanteil.

 

Spätestens hier entsteht die Frage, was die höheren Subsysteme des Gehirns mit dem Output der vielen primären Cortexcluster anstellen. Es ist anzunehmen, dass dieser Output in den Assoziativgebieten der Cortexrinde weiterverarbeitet wird.

Insofern besteht die Hauptaufgabe des Striosomensystems und der Cortexcluster offenbar darin, zunächst einmal die wesentlichen Signalkombinationen zu ermitteln und als selbständige Signale zu definieren.

 

Obwohl es uns erscheinen mag, dass wir die Funktion des Cerebellums verstanden hätten, sind wir dennoch erst am Anfang unserer Erkenntniskette. Denn nunmehr ergibt sich die Frage, welche Signale das Cerebellum konkret verarbeitet und welche Elementarsignale sich in ihm zu neuen Komplexsignalen verknüpfen.

Bisher haben wir nur die Wirkung der Kletterfasern analysiert, die vom magnocellularen System des Gehirns bereitgestellt werden. Hier war das Striosomensystem der Basalganglien bedeutungsvoll. Es liefert den neuronalen Systemtakt, den ersten Hinweis auf computerähnliches Arbeiten. Und es liefert das magnocellulare Kletterfasersignal als neuronalen Schreibbefehl. Dies ist der zweite Hinweis auf computerähnliche Funktionsweise. Nun ist es an der Zeit, die übrigen Kletterfasersysteme des Säugergehirns zu analysieren. Hier stehen uns weitere wichtige Einsichten bevor.

• ← Teil 1.6. Die neuronalen Elementarschwingkreise im Striosomensystem
• Index
• Teil 2.1. Das parvocellulare Kletterfasersystem des Gehirns →

---

ISBN 978-3-00-037458-6
ISBN 978-3-00-042153-2

Monografie von Dr. rer. nat. Andreas Heinrich Malczan