Theorie der neuronalen Schaltung des Gehirns
und des analytischen Denkens
ISBN 978-3-00-037458-6ISBN 978-3-00-042153-2
Monografie von Dr. rer. nat. Andreas Heinrich Malczan
Teil 2.11. Die Grundschaltung der inneren Leinwand als inverses Erkennungsgitter
Ein Vorzug unseres Denkapparates ist die Möglichkeit, sich etwas Reales oder Gedachtes vorzustellen. Besonders realitätsnah sind Traumerlebnisse. Hier haben wir die Illusion, das Geträumte sei handfeste Realität. Nur selten erkennt man im Traume, dass man selbst träumt. Es wäre der krönende Abschluss dieser Monografie, wenn es dem Autor gelänge, die schaltungstechnische Realisierung der -inneren Leinwand- aufzuzeigen. Selbst wenn es nur ein vorläufiges Modell wäre.
Den Lesern dieses Abschnittes sei Geduld empfohlen. Und alle Mathematiker und Physiker unter ihnen seien aufgerufen, die vorgestellte Schaltung aus systemtheoretischer Sicht zu analysieren. Die Funktionsfähigkeit steht im Vordergrund.
Neurologen sollten die aufgezeigten Schaltungswege (Projektionswege) kritisch, aber wohlwollend prüfen und hinterfragen.
Obwohl die zugehörige wissenschaftliche Anwendung erst im dritten und vierten Teil dieser Monografie vorgesehen ist, soll ein kurzer Einblick in das theoretische Konzept des Autors gegeben werden. Die erste reale Vorstellung über die Arbeitsweise intelligenter Systeme erhielt der Autor dieser Monografie vor vielen Jahren, als er erstmalig erkannte, wie zwei kybernetische Systeme miteinander kommunizieren könnten. Während das eine System Signale aussendet, werden diese vom anderen System empfangen und interpretiert. Anschließend antwortet dieses System, während das andere empfängt. Als Kommunikationsmittel bevorzugte der Autor die reale Sprache.
Wie läuft so ein Kommunikationsprozess (rein theoretisch) ab?
Zunächst sendet System A und System B empfängt. Dazu wandelt System B den empfangenen Schall in Binärdaten um. Anschließend spricht das System B zum System A. Dazu ruft es zunächst die zwischengespeicherten Binärdaten ab, die anschließend als Schall ausgesendet werden.
Es gibt also eine Empfängerschaltung und eine Sendeschaltung. Der Autor dieser Monografie erkannte irgendwann, dass diese zwei Schaltungen zueinander invers waren. Die eine wandelt Schall in Binärdaten um, die andere transformiert Binärdaten in Schall.
Ein mechanisches Analogon ohne binäre Arithmetik war die Erfindung der Schallplatte.
Zunächst bewegt der Schall über eine geeignete Membran eine Nadel, die die Schallwellen in eine rotierende Wachsscheibe eingraviert, also speichert. Beim inversen Vorgang bewegt sich die Nadel in den bereits eingravierten Rillen der sich drehenden Wachsplatte und bewegt eine Membran, die diese Bewegungen als Schallwellen an die Luft abgibt. Und damit die Wachsplatte sich nicht so schnell abnutzt, ersannen Techniker die Möglichkeit, diese Rillen in widerstandsfähigere Plaste zu übertragen. Die Schallplatte war geboren. Deutlich wird, dass das Aufzeichnen des Schalls und das Abspielen der Schallplatte zueinander inverse Vorgänge sind.
In der Elektronik gibt es viele Anwendungen dieser Art. Rundfunksender wandeln Schall in elektromagnetische Wellen, die vom Radioempfänger wieder in Schallwellen umgewandelt werden. So kann ein Orchester gleichzeitig hunderttausende Hörer erfreuen. Solche Schaltungen wollen wir als zueinander inverse Schaltungen bezeichnen.
Nach Ansicht des Autors gibt es im Gehirn zu fast jeder neuronalen Schaltung eine inverse Schaltung, bei der also die Rolle von Input und Output vertauscht ist.
Einige Beispiele seien einfach genannt, obwohl ihre Erklärung teilweise erst im Teil 3 und 4 dieser Monografie erfolgen wird.
|
konvergente Schaltung |
divergente Schaltung |
|
direkte neuronale Schaltung |
inverse neuronale Schaltung |
|
Schwerpunktgitter |
inverses Schwerpunktgitter |
|
Interpolationsgitter |
inverses Interpolationsgitter |
|
Assoziativmatrix |
inverse Assoziativmatrix |
|
Cortex |
inverser Cortex |
|
Cerebellum |
inverses Cerebellum |
Der Autor ist der festen Überzeugung, dass es fast zu jeder neuronalen Schaltung eine inverse Schaltung gibt, die auch real im Gehirn existiert.
Beispielsweise gibt es Cortexareale, die ihren Input vom Thalamus erhalten und als divergente Schaltung zu jedem Inputneuron sehr viele Outputneuronen aufweisen. Andererseits gibt es Cortexareale, die relativ viele Inputneuronen besitzen, aber deutlich weniger Outputneuronen enthalten. Die motorischen Areale mit den Beetzschen Riesenzellen zählt der Autor zu dieser Kategorie. Er interpretiert diese Gebiete als inversen Cortex. Doch dazu mehr in Teil 3 und 4 dieser Monografie, die erst entstehen müssen. Wir konzentrieren uns hier auf die Theorie eines inversen Cerebellums.
Wenn der Videospeicher im Cerebellum eine Schaltungsart ist, muss es nach Ansicht des Autors die dazu inverse Schaltung geben. Die wäre beispielsweise dazu da, einen im Cerebellum gespeicherten Film abzuspielen, so dass wir ihn vor unserer inneren Leinwand sehen. Zum Beispiel während des Schlafes, quasi als Traumerlebnis.
Dass dieses inverse Cerebellum noch ganz andere reale Aufgaben zu bewältigen hat, wird sich wahrscheinlich im dritten und vierten Teil der Monografie noch zeigen. Insbesondere beruht die komplette Motorik auf dem Zusammenspiel von direkten und inversen Schaltungen, in die zusätzlich intelligenzspendende neuronale Netze und Assoziativmatrizen eingebunden sind. Besonders interessant dürfte für Mathematiker eine inverse Assoziativmatrix sein. Die Hintereinanderschaltung einer Assoziativmatrix und einer dazu inversen Assoziativmatrix ergibt als Output den ursprünglichen Input. Die Hintereinanderschaltung wirkt also als Einsmatrix, als neutrales Element. Hier wird vielleicht ein neues Teilgebiet der Algebra - die Signalalgebra - geboren.
Gehen wir also an die Erklärung des inversen Cerebellums und der inneren Leinwand.
Wir haben erkannt, dass man primäre und sekundäre Cortexcluster unterscheiden kann. Jede Clusterart erzeugt über das Matrixsystem parvocellulare Kletterfasern.
Die parvocellularen Kletterfasern des Matrixsystems des sekundären Cortexclusters koppeln an die zugehörigen Purkinjegruppen des primären Cerebellums an und substituieren dort das magnocellulare (striosomale) Kletterfasersignal. Dadurch wird das primäre Cerebellum zur Nachprägung fähig. Lernvorgänge werden während der Gesamtlebenszeit des Individuums möglich.
Wir fragen nunmehr, welche Funktion die parvocellularen Kletterfasern haben, die vom Matrixsystem aus den Signalneuronen des primären Cortex abgeleitet werden. An welchen Purkinjegruppen werden diese Kletterfasern andocken?
Aus systemtheoretischer Sicht hat der Autor dieser Monografie nur eine mögliche Variante: Die vom primären Cortexcluster über das Matrixsystem abgeleiteten parvocellularen Kletterfasern ziehen zum sekundären Cerebellum. Dort annektieren sie freie Purkinjegruppen, um sie mit ihrer Kletterfaseraktivität zu prägen.
Diese Purkinjegruppen sind dann markerverwandt mit den Signalneuronen des primären Cortex. Jedes Signalneuron übergibt seine persönliche, individuelle Markerkombination an die angeschlossenen Matrixneuronen, die wiederum eine parvocellulare Kletterfaser mit dieser Markerkombination erzeugen. Diese annektiert im sekundären Cerebellum eine freie Purkinjegruppe und übergibt dabei auch die Markerkombination, also den persönlichen Erkennungscode des ursprünglichen Signalneurons des primären Cortex an die annektierte Purkinjegruppe. Daher kann der Output der Purkinjegruppe vermittels des Markers das ursprüngliche Signalneuron suchen. Das positive Kernneuron projiziert in den Thalamus und dockt dort genau an das Thalamusneuron an, dessen Signal zum ursprünglichen Signalneuron führt. Damit schließt sich der Kreis.
Somit gibt es im sekundären Cerebellum zwei Arten von Purkinjegruppen. Die eine Art erhält ihre parvocellularen Kletterfasern vom Matrixsystem des sekundären Cortex. Diese Purkinjegruppen bilden nach Ansicht des Autors das direkte Cerebellum. Ihre Aufgabe ist die Nachprägung der Eigensignale der Purkinjegruppen.
Die andere Art von Purkinjegruppen erhält ihre parvocellularen Kletterfasern vom Matrixsystem des primären Cortex. Sie bilden nach der Theorie des Autors das inverse Cerebellum. Wir fassen dies zunächst in eine Definition.
Definition 2.14: Direktes und inverses Cerebellumcluster
Der direkte Cerebellumcluster wird von denjenigen Purkinjegruppen gebildet, die ihren Moosfaserinput unter Einschaltung der Brückenkerne vom primären Cortexcluster beziehen, deren striosomales Erstprägungs-Kletterfasersignal vom Aktivitätsneuron des primären Cortexclusters stammt und deren parvocellulare Nachprägungs-Kletterfasern das Matrixsystem von den Signalneuronen des sekundären Cortexclusters ableitet. Den zugehörigen Cerebellumkern bezeichnen wir als direkten Cerebellumkern.
Der inverse Cerebellumcluster wird von denjenigen Purkinjegruppen gebildet, die ihren Moosfaserinput unter Einschaltung der Brückenkerne vom sekundären Cortexcluster beziehen und deren parvocellulare Kletterfasern das Matrixsystem von den Signalneuronen des primären Cortexclusters ableitet. Den zugehörigen Cerebellumkern bezeichnen wir als inversen Cerebellumkern.
Definition 2.15: Direktes und inverses Cerebellum
Die Gesamtheit der direkten Cerebellumcluster bildet das direkte Cerebellum. Die Gesamtheit der inversen Cerebellumcluster bildet das inverse Cerebellum.
Damit haben wir zwar den Begriff des inversen Cerebellums definiert, jedoch noch nicht bewiesen, dass dieses als neuronale Schaltung die inverse Schaltung des direkten Cerebellums ist. Diesen Nachweis werden wir nun erbringen. Gewiss könnte der Beweis einfacher, einleuchtender oder gar ästhetisch schöner geführt werden. Aber wir kämpfen hier nicht um einen Schönheitspreis, sondern um die Fehlerfreiheit des Beweises.
Die Frage ist, welche Behauptung wir eigentlich beweisen wollen. Hier muss der Leser sich auf die Intuition des Autors verlassen.
Die Inspiration dazu lieferte dem Autor das überaus spannende Werk "Das Gehirn" von Richard F. Thompson vom Spektrum Akademischer Verlag, das überdies auch höchst amüsant zu lesen ist, wie nachfolgend gezeigt wird.
Auf Seite 266 ist diejenige Stelle zu finden, die den Autor erstmalig inspirierte, ein inverses System im Gehirn anzunehmen, dessen Aufgabe es war, Illusionen zu erzeugen.
Wir lesen dort über das visuelltemporale Feld VTE die nachfolgende Anekdote:
(Zitatbeginn:)
"Die Entdeckung, dass das VTE-Feld eine ganz bestimmte Art von visueller Information empfängt, war ein klassischer wissenschaftlicher Glücksfall. So wie die Geschichte erzählt wird, untersuchten Charles Gross und seine Kollegen an der Harvard-Universität an Affen die Reaktionen von Zellen im VTE-Feld auf visuelle Reize. Sie verwendeten Lichtpunkte, Kanten und Balken - die üblichen Standardreize. Die Nervenzellen in der VTE-Region reagierten ein klein wenig auf diese einfachen Reize, nicht jedoch auf Berührungen oder auf Töne. So erschien es den Wissenschaftlern zwar, dass diese Region ein visuelles Feld sei, aber kein sehr ausgeprägtes. Nachdem sie eine bestimmte Zelle lange mit nur minimalen Ergebnissen untersucht hatten - die Zelle reagierte kaum auf ihre Reize -, entschlossen sie sich, es mit einer anderen zu versuchen. Als Geste zum Abschied von dieser Zelle hob einer der Wissenschaftler die Hand vor dem Auge des Affen und winkte. Die Zelle feuerte plötzlich wie wild. Man braucht eigentlich nicht zu erwähnen, dass die Wissenschaftler bei dieser Zelle blieben. Sie schnitten sofort verschiedene Handumrisse aus Papier aus und probierten sie aus. Die Zelle mochte offenbar eine erhobene Hand in Form einer Affenhand am liebsten. Die Zellen im visuellen Feld VTE scheinen am besten auf spezifische, komplexe Umrisse zu reagieren. Einige Neuronen in diesem Feld reagieren selektiv auf Affengesichter, vermutlich analog zu dem Bereich der beim Menschen für das Erkennen von Gesichtern zuständig ist"
(Zitatende)
Dieses Beispiel zeigt deutlich, wie spannend und teils auch erheiternd neurologische Forschung sein kann.
Was aber hat die dargestellte selektive Fähigkeit der Neuronen im Feld VTE - dem visuelltemporalen Feld - mit dem inversen Cerebellum zu schaffen?
Der Autor ist fest davon überzeugt, dass das erwähnte "Affenhandneuron" aus obigem Zitat immer stark feuerte, wenn der Affe in seinem sichtbaren Sehfeld eine echte Affenhand oder wenigstens eine Attrappe davon sah. Davon konnten sich die beteiligten Wissenschaftler durch das Experiment tatsächlich überzeugen.
Aber der Autor geht noch einen Schritt weiter. Er unterstellt die Behauptung, dass eine künstliche, externe elektronische Reizung des "Affenhandneurons" vermittels einer kleinen Elektrode dem Affen die Illusion verschafft hätte, eine Affenhand wäre in seinem Gesichtsfeld aufgetaucht.
Die Begründung ist einfach, muss aber bewiesen werden.
Bekannt ist bereits, dass die elektrische Reizung von Neuronen des Cortex oder anderer Regionen von den beteiligten Versuchspersonen so beschrieben wird, dass bestimmte Empfindungen, Wahrnehmungen, ja Halluzinationen auftreten. Der Autor unterstellt, dass es ausreicht, ein Neuron extern elektronisch zu reizen, anstatt das Nervensystem mit demjenigen realen Reiz zu konfrontieren, bei dem genau dieses Neuron feuert. Das Neuron erkennt nicht nur ein ihm zugeordnetes Komplexsignal, sondern seine externe elektronische Reizung ruft im Nervensystem die Illusion hervor, das Komplexsignal wäre tatsächlich vorhanden.
Ähnlich ist es im Traum. Hier wird die Illusion perfekt.
Wir wollen die neuronale Schaltung dazu vorstellen und diese These beweisen. Dieses Mal werden wir mathematisch vorgehen und die Behauptung dem Beweis voranstellen.
Zunächst erscheint es sinnvoll, den Begriff des Komplexneurons zu definieren.
Definition 2.16: Komplexneuron und sein Komplexsignal
Jedes Signalneuron des sekundären Cortex bezeichnen wir als Komplexneuron. Es ist genau dann aktiv, wenn das ihm zugeordnete Komplexsignal auf den primären Cortex einwirkt.
Wir rekapitulieren: Jedes Komplexneuron wird von genau einem Neuron des sekundären Thalamus erregt. Dieses Thalamusneuron wiederum erhält sein erregendes Inputsignal vom positiven Kernneuron des primären Cerebellums genau dann, wenn die zugehörige Purkinjegruppe ihr Eigensignal erkannt hat. Dieses Eigensignal wird erkannt, wenn das zugehörige Komplexsignal auf den primären Cortex wirkt und seine aktiven Signalneuronen genau die Moosfasern im primären Cerebellum erregen, die zum Eigensignal der Purkinjegruppe zählen. Somit sind das Eigensignal der Purkinjegruppe, das Komplexsignal im primären Cortex und das dem Komplexneuron zugeordnete Komplexsignal identisch.
Nach diesen Vorbemerkungen ist nun der Beweis zu führen. Zu beweisen ist folgende Behauptung des Autors:
(Beginn der Behauptung:)
Wenn ein prägungsfähiges, bisher aber nicht geprägtes Komplexsignal K, bestehend aus k aktiven Elementarsignalen, von beliebigen Rezeptoren R1, R2, R3, ..., Rk des System kommend
a) im primären Thalamus die zugehörigen k Neuronen T1, T2, T3. ..., Tk erregt,
b) diese aktiven Thalamusneuronen ihrerseits die zugehörigen k Neuronen C1, C2, C3, ..., Ck im primären Cortex erregen,
c) wenn genau diese Cortexneuronen k zugehörige Neuronen B1, B2, B3, ..., Bk der Brückenkerne erregen,
d) wenn diese Brückenkernneurone ihrerseits die ihnen zugeordnete Moosfasern M1, M2, M3, ..., Mk des zugehörigen Cerebellumclusters erregen
e) wenn diese aktiven Moosfasern im Cerebellum eine freie Purkinjegruppe PGK erregen, während das vom Aktivitätsneuron des Cortexclusters abgeleitete Kletterfasersignal diese Purkinjegruppe mit genau diesem Komplexsignal K prägt, so dass deren positives Kernneuron im sekundären Thalamus ein Komplexneuron TS,K immer dann erregt, wenn das Komplexsignal K aktiv ist
f) wenn dieses Neuron des sekundären Thalamus im Aktivitätsfall ein Neuron N des sekundären Cortex erregt, wenn das Komplexsignal K aktiv ist
g) wenn dieses Neuron N des sekundären Cortex im Aktivitätsfall eine Moosfaser MK des sekundären Cerebellums aktiviert,
h) und wenn zusätzlich jedes zum Komplexsignal gehörende aktive Signalneuron des primären Cortex C1, C2, C3, ..., Ck über das Matrixsystem der Basalganglien eine Kletterfaser F1, F2, F3, ..., Fk generiert, von denen jede im sekundären Cerebellum eine eigene Purkinjezelle P1, P2, P3, ..., Pk okkupiert und geprägt hat, die wir als Elementarsignal-Purkinjezellen bezeichnen,
i) wenn jede dieser Purkinjezellen P1, P2, P3, ..., Pk sowohl von der Moosfaser MK als auch von der zugehörigen Kletterfaser F1, F2, F3, ..., Fk aktiviert wird, so dass es zur Prägung kommt,
j) wenn diesen Elementarsignal-Purkinjezellen im (inversen) sekundären Cerebellumkern die Kernneuronen K1, K2, K3, ..., Kk zugeordnet sind,
k) wenn jede dieser Elementarsignal-Purkinjezellen Ki im primären Thalamus das Neuron Ti kontaktiert und im Aktivitätsfalle erregt,
l) so wird immer dann, wenn im sekundären Cortex das Komplexneuron N extern über eine Elektrode gereizt wird, aber das Komplexsignal K nicht auf die Rezeptoren R1, R2, R3, ..., Rk des Nervensystems einwirkt
der primäre Thalamus über die positiven Kernneuronen K1, K2, K3, ..., Kk der genannten Elementarsignal-Purkinjezellen mit dem gleichen Komplexsignal K versorgt, welches er erhalten hätte, wenn das reale Komplexsignal K die Rezeptoren R1, R2, R3, ..., Rk des Nervensystems tatsächlich gereizt hätte.
(Ende der Behauptung)
Die externe, elektronische Reizung des Neurons N im sekundären Cortex bewirkt einen Moosfaserinput auf die Elementarsignal-Purkinjezellen. Der Output ihrer positiven Kernneuronen versorgt den primären Thalamus mit dem gleichen Input, den auch ein externes Komplexsignal erzeugen würde, wenn es vorhanden wäre. Somit entsteht im primären Thalamus die Illusion eines Signals, welches es in Wirklichkeit nicht gibt.
Wir schreiten nun zum Beweis.
Es mögen k aktive Rezeptoren ihre Signale als Komplexsignal an den primären Thalamus senden und dort k Thalamusneuronen erregen. Der Rezeptor Rm möge das Thalamusneuron Tm erregen.
Jedes Thalamusneuron Tm projiziert in den primären Cortex und erregt dort ein Cortexneuron Cm.
Jedes der k Cortexneuron projiziert in ein Brückenkernneuron, wobei das Cortexneuron Cm in das Brückenkernneuron Bm projiziert und dieses erregt.
Jedes Brückenkernneuron projiziert in eine Moosfaser des primären Cerebellums, wobei das Brückenkernneuron Bm in die Moosfaser Mm projiziert.
Da das auf den Thalamus einwirkende Komplexsignal K prägungsfähig ist und die Prägung bereits vollzogen wurde, existiert im primären Cerebellum genau eine Purkinjegruppe G, deren Eigensignal das über die Brückenkerne eintreffende Moosfasersignal ist. Solange K aktiv ist, erkennt die Purkinjegruppe dieses Eigensignal.
Die erkennende Purkinjegruppe besitzt ein positives Kernneuron, welches im hier vorliegenden Erkennungsfall stark erregt ist und seine Erregung über den sekundären Thalamus zu einem Neuron N des sekundären Cortex weiterleitet. Daher ist dieses Cortexneuron N ebenfalls stark erregt, solange das Komplexsignal K auf den Thalamus einwirkt.
Dieses Cortexneuron N erregt über die Brückenkerne eine Moosfaser im sekundären Cerebellum, die ihrerseits eine Parallelfaserschaar (mit geringer Zeitverzögerung) immer dann aktiviert, wenn das Komplexsignal K auf den Thalamus einwirkt.
Die k Cortexneuronen C1, C2, C3, ... , Ck des primären Cortex senden ihren Input auch an das Matrixsystem des Striatums. Dort entstehen k parvocellulare Kletterfaseraxone K1, K2, K3, ..., Kk, die laut Voraussetzung zum sekundären Cerebellum ziehen und dort k Purkinjegruppen okkupieren. Jede dieser Kletterfasern ist (mit geringer Zeitverzögerung) genau dann aktiv, wenn das Komplexsignal K des primären Cortex aktiv ist. Genau dann sind aber auch die genannte Moosfaser und die zugehörige Parallelfaserschaar aktiv.
Daher werden im sekundären Cerebellum genau k Purkinjegruppen geprägt, wenn das Komplexsignal K erstmals hinreichend lange aktiv ist. Dies trifft zu, denn dieses Komplexsignal ist laut Voraussetzung prägungsfähig.
Jede der k geprägten Purkinjegruppen erhält einen Parallelfaserinput von der Parallelfaserpopulation, die vom Komplexsignal aktiviert wird.
Andererseits erhält jede dieser Purkinjezellen je ein Kletterfasersignal, welches von den beteiligten k Signalneuronen dem primären Cortex abgeleitet wird. Dazu wird der Output dieser Signalneuronen, die ja nach Voraussetzung aktiv sind, im Matrixsystem der Basalganglien in k aktive Kletterfasersignale umgewandelt, welche nun die genannten Purkinjegruppe prägen.
Nach dieser Prägung wird jede dieser geprägten Purkinjegruppen genau dann ihr Eigensignal erkennen, wenn das Komplexsignal K im Thalamus aktiv ist und dadurch das Neuron N im sekundären Cortex aktiviert, damit dessen Axon über die Brückenkerne die genannte Parallelfaserpopulation erregen kann.
Die Erregung der Parallelfaserschaar ist aber für die genannten Purkinjegruppen der Anlass, dieses Eigensignal zu erkennen und ihrerseits über ihre positiven Kernneuronen den primären Thalamus zu erregen. Hierbei erregt das i-te Kernneuron Ki das i-te Thalamusneuron Ti.
Wenn nundas Neuron N des sekundären Cortex - wie vorausgesetzt - nicht vom Thalamus erregt wird, sondern mittels einer externen Elektrode gereizt wird, so wird seine Erregung ebenfalls über die Brückenkerne die gleiche Parallelfaserpopulation erregen, die bei den genannten Purkinjegruppen die Signalerkennung als Eigensignal bewirkt. Daher werden die positiven Kernneuronen dieser Purkinjegruppen den primären Thalamus ebenso erregen, wie es das ursprüngliche reale Komplexsignales getan hätte. Nur dass in diesem Falle eine Elektrode die Reizung des Neurons N bewirkt.
Der Thalamus kann nicht unterscheiden, von wem er erregt wurde:
- Waren es die Rezeptoren R1, R2, R3, ..., Rk, die ihn erregten?
- Oder waren es die k Outputaxone der positiven Kernneuronen derjenigen Elementarsignal-Purkinjezellen des inversen Cerebellums, deren Kletterfasern von den Signalneuronen T1, T2, T3, ..., Tk des primären Thalamus stammten und deren Moosfaserinput vom künstlich gereizten Neuron N des sekundären Cortex kam?
Selbstverständlich muss es nicht unbedingt eine externe Erregung mit Hilfe einer Elektrode sein, die eine geeignete Erregungsspannung an das zu reizende Neuron anlegt. Jedes Neuron kann auch von den übergeordneten Systemen gereizt werden. Denn das Prinzip der inneren Abbildung ist rekursiv. Es beruht aus systemtheoretischer Sicht aus der Hintereinanderschaltung einer Assoziativmatrix und einer inversen Assoziativmatrix. Deren Output ist das Ursprungssignal, und es wird nach der vorgelegten Schaltung genau den Thalamusneuronen zugeführt, die auch die Ursprungssignale erhalten. Wir fassen diese Erkenntnis in ein eigenes Theorem. Es ist ein rein abstraktes informationstheoretisches Theorem, welches unabhängig von der realen neuronalen Schaltung des Gehirns gilt. In Klammern gesetzt sind die realen neurologischen Bezüge - eher zum leichteren Verständnis. Dieses Theorem benennt der Autor nach der Stadt Ulm, weil von der Universität Ulm die erste zustimmende Rückmeldung zur ersten Fassung dieser Monografie kam. Auf irgendeine Reaktion aus Tübingen wartet der Autor dagegen bis heute vergeblich.
Theorem 2.28: Theorem von Ulm
Führt ein Inputsystem (der Thalamus) seine Originalsignale einer Schaltung zu, die aus der Hintereinanderschaltung einer Assoziativmatrix (dem direkten Cerebellumcluster) und einer inversen Assoziativmatrix (dem inversen Cerebellumcluster) besteht, so erzeugt diese Schaltung (für eine gewisse Inputmenge) als Output wieder die Originalsignale. Wird der Output der Hintereinanderschaltung wieder dem Inputsystem (dem Thalamus) als Input zugeführt, so ist das System nicht fähig, einen Fremdinput in die inverse Assoziativmatrix vom einen Originalinput in das Inputsystem zu unterscheiden. Ein Fremdinput in die inverse Assoziativmatrix gaukelt dem System einen realen Input im Inputsystem (dem Thalamus) vor, weil das inverse System genau einen solchen Input zum Thalamus sendet. Darauf beruht die -innere Leinwand-, das -innere Auge des Betrachters- und die Vorstellungskraft und Phantasie des Menschen und der Tiere.
Deutlich muss vermerkt werden, dass das Theorem von Ulm noch tiefer aufgearbeitet werden muss. Denn Assoziativmatrizen reagieren auch auf Input, der neben den zu erkennenden Eigensignalen auch Fremdsignalanteile enthalten darf. Daher ist der einschränkende Begriff der "gewissen Inputmenge" durch weitere Forschung näher zu präzisieren. Für Systemtheoretiker und Informationstheoretiker liegt hier ein noch unbestelltes Feld vor, welches es zu beackern gilt. Vielleicht verfügt die Universität von Ulm sowohl über die Kapazität als auch über die Initiative, diese Thematik aufzugreifen und zu bearbeiten.
Da das Cerebellum eine Assoziativmatrix darstellt, erlaubt sich der Autor, das inverse Cerebellum als inverse Assoziativmatrix zu bezeichnen, da es ebenfalls eine Assoziativmatrix ist. Dies bedeutet aber nicht, dass die Assoziativmatrix und ihre inverse Assoziativmatrix bezüglich der Matrizenaddition oder der Matrizenmultiplikation zueinander invers wären. Die Inversität liegt hinsichtlich der Hintereinanderausführung vor, die jedoch weder eine Addition bzw. Subtraktion noch eine Multiplikation bzw. Division darstellt. Später wird sich zeigen, dass das Cerebellum schaltungstechnisch einen Spezialfall eines Adressdekodierers darstellt, während das inverse Cerebellum einen speziellen Adresskodierer repräsentiert.
Bedeutsam erscheint dem Autor die Möglichkeit, dass der Input in das inverse System nicht unbedingt durch externe elektronische Reizung der Neuronen mit Elektroden hervorgerufen werden muss. Auch die höheren Systeme haben wiederum inverse Komponenten, über die sie auf die genannten Neuronen zugreifen können.
Daher muss man sich nun fragen, warum wir nicht ständig an Halluzinationen leiden, weil irgendwelche Neuronen des sekundären Cortex zum Beispiel von übergeordneten Teilsystemen erregt werden. Hier greift die rezeptive Nachbarhemmung der Thalamusneuronen aktiv ins Geschehen ein. Bekanntlich befinden sich im Thalamus jede Menge hemmender Interneuronen. Daher setzen sich die stärkeren Signale durch. Der Output der Purkinjegruppen des inversen Cerebellums ist relativ schwach, da immer nur eine Parallelfaserpopulation von vielen möglichen erregt ist. Daher fällt das inverse Signal im Allgemeinen durch das Erregungsraster und wird nicht sonderlich wahrgenommen.
Anders in Ruhe oder Reizarmut. Da erscheinen plötzlich -Gedanken, Bilder oder sogar innere Eingebungen- aus dem Nichts. Dies ist kein Zeichen von Krankheit, sondern das Resultat unseres inversen Cerebellums. Es vermag Signale der übergeordneten Sphären in unsere -innere Ansicht- oder unser "inneres Auge" zu transformieren.
Daher gilt das nachfolgende Theorem.
Theorem 2.29: Rezeptive Nachbarhemmung im Thalamus
Die rezeptive Nachbarhemmung im Thalamus ist auch notwendig, weil das inverse System den Thalamus mit Input beliefert. Sie stellt sicher, dass die jeweils stärksten Signale sich gegenüber den schwächeren durchsetzen.
In Kapitel 3 wird sich zeigen, dass die rezeptive Nachbarhemmung - bei der jedes Outputneuron jedes Outputneuron relativ zu seiner Feuerrate hemmt - ein Grundprinzip aller Erkennungsgitter ist.
Erwähnt werden sollte, dass die rezeptive Nachbarhemmung nicht nur im Thalamus vorkommt. So gibt es in allen Kleinhirnkernen hemmende Interneuronen, die offenbar für eine rezeptive Nachbarhemmung sorgen. Ob diese rezeptive Nachbarhemmung generell zwischen den Outputneuronen wirkt, möge die Forschung abklären.
Ebenfalls in Teil 3 und 4 dieser Monografie wird (voraussichtlich) aufgezeigt, wie das inverse Cerebellum genutzt werden kann, um Antworten auf Fragen zu finden. Vorausgesetzt, es interessiert sich jemand dafür.
Wir fassen unsere Erkenntnis zum inversen Cerebellum wie üblich in ein neues Theorem. Als Inhaber der Urheberrechte beschließt der Autor, genau dieses Theorem zu Ehren seiner polnischen Geburtsstadt als das Theorem von Nowy Bytom zu bezeichnen.
Theorem 2.30: Theorem von Nowy Bytom
Das inverse Cerebellum als Teil des sekundären Cerebellums ist fähig, eine natürliche oder künstliche Erregung eines Signalneurons im sekundären Cortex, dem ein Komplexsignal K entspricht, wieder in die Elementarsignale dieses Signals zu transformieren derart, dass diese genau diejenigen Signalneuronen des Thalamus erregen, die eine natürliche Erregung des neuronalen Systems mit diesem Komplexsignal hervorgerufen hätte.
Im Gegensatz zum Theorem von Ulm, welches das informationstheoretische Prinzip der Hintereinanderschaltung von Assoziativmatrix und inverser Assoziativmatrix rein abstrakt analysiert, erklärt das Theorem von Nowy Bytom die konkrete Realisierung im (menschlichen) Gehirn.
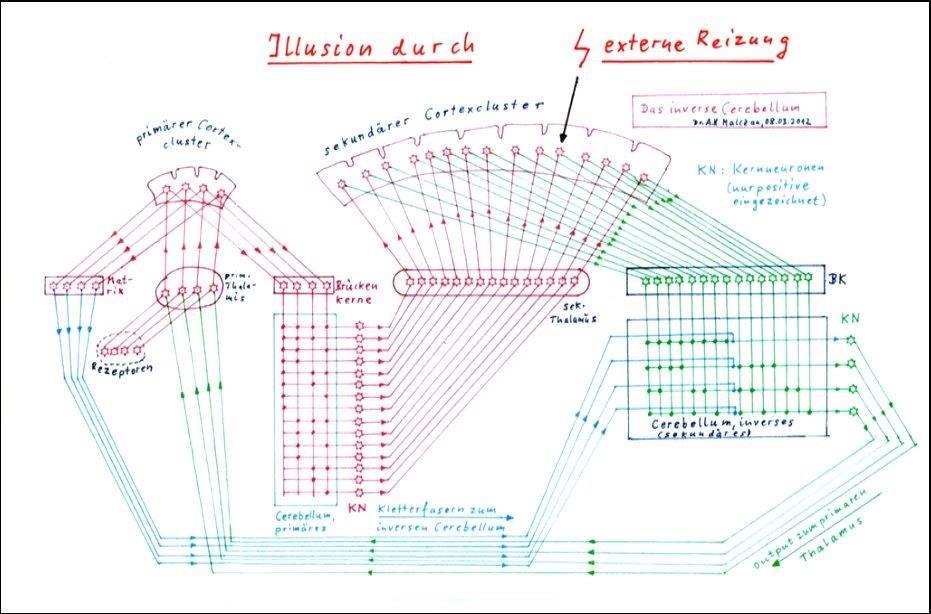
In der Skizze auf der nachfolgenden Seite wird die Grundschaltung der inneren Leinwand aufgezeigt. Links beginnt die Signalverarbeitung mit dem Input, den die Rezeptoren zum primären Thalamus senden. Es sind beispielhaft nur 4 Rezeptoren eingezeichnet, obwohl ein Cortexcluster bestimmt von einigen Hundert Inputrezeptoren versorgt wird.
Der Input steigt zum primären Cortexcluster empor und erregt die zugehörigen vier Signalneuronen. Diese beliefern mit ihrem Output zwei Teilsysteme: das Matrixsystem (links vom primären Thalamus eingezeichnet) und die Brückenkerne (rechts eingezeichnet).
Die Brückenkerne beliefern ihrerseits das primäre und direkte Cerebellum. Eingezeichnet sind symbolisch die Synapsen der 15 Purkinjegruppen als Punkte sowie die positiven Kernneuronen. Es wäre an dieser Stelle zu viel verlangt, 15 komplette Purkinjegruppen mit beispielsweise je drei Purkinjezellen in diese Darstellung einzuzeichnen, weil dann die Übersicht komplett verloren ginge.
Mit etwas gutem Willen erkennen Mathematiker im primären Cerebellum bereits die digitale Signatur der abgespeicherten Eigensignale. Ein fett gezeichneter Kreuzungspunkt entspricht einer binären Eins, ein fehlender dem Binärwert Null. Zu vier Elementarsignalen des primären Thalamus gibt es hier 15 nichttriviale Komplexsignale.
Der Output der positiven Kernneuronen zieht zum sekundären Cortex. Dessen Output erreicht die Brückenkerne und vier zugehörige Purkinjegruppen im inversen Cerebellum.
Die Kletterfasern für diese vier Purkinjegruppen stammen vom Matrixsystem des primären Cortex (blau eingezeichnet). Das inverse Cerebellum ist im Vergleich zum direkten Cerebellum invers geprägt. Input sind die 15 Komplexsignale, Output die vier Elementarsignale.
Reizt nun ein externes Signal (wie eingezeichnet) ein Komplexneuron des sekundären Cortex, so transformiert das sekundäre Cerebellum diesen Input wieder in seine ursprünglichen Elementarsignale und sendet diese an den primären Thalamus. Dort entsteht die Illusion, das Komplexsignal wäre real vorhanden. In Wirklichkeit aber wird nur ein Neuron des sekundären Cortex gereizt.
Während in der Skizze 2.8 auf der folgenden Seite das Matrixsystem des primären Cortexclusters eingezeichnet ist und seine Kletterfasern zum sekundären, inversen Cerebellum sendet, ist das komplette Matrixsystem des sekundären Cortexclusters mit seinen 15 (Beispielwert) Kletterfasern, die der Nachprägung im primären Cerebellum dienen, aus Gründen der Übersichtlichkeit nicht eingezeichnet.
Skizze 2.8: Die Entstehung von Illusionen - Das inverse Cerebellum - Die innere Leinwand
Damit unterteilt diese Theorie das Cerebellum je nach der Herkunft der Kletterfasern in zwei Teilcerebelli: das direkte Cerebellum und das inverse Cerebellum. Ebenso werden nun zwei Kleinhirnkerne unterschieden.
Während im direkten Cerebellum die Komplexsignale gespeichert werden, werden im inversen Cerebellum die Elementarsignale gespeichert. Da es zu den Elementarsignalen des primären Cortex immer viel mehr Komplexsignale gibt, besitzt das direkte Cerebellum deutlich mehr Purkinjegruppen als das inverse Cerebellum.
Jedes Elementarsignal kann aktiv oder passiv sein, also durch Eins oder Null repräsentiert werden. Zu zwei Elementarsignalen gibt es bereits vier Kombinationen: 00, 01, 10 und 11. Zu 4 Elementarsignalen gibt es rein theoretisch 16 Komplexsignale, zu 5 Elementarsignalen bereits 32. Zu n Elementarsignalen gibt es 2n Komplexsignale. Wenigstens rein theoretisch, denn nicht jede der Signalkombinationen aus Elementarsignalen kommt im realen Leben vor.
Wären alle Signalkombination möglich, so wären einem inversen Cerebellum aus n Purkinjegruppen ein direktes Cerebellum mit 2n Purkinjegruppen zugeordnet.
Theorem 2.31: Potenzierungstheorem
Zu n Elementarsignalen des inversen Cerebellums gibt es maximal 2n mögliche Komplexsignale, wenn jedes Elementarsignal nur die Werte aktiv oder inaktiv annehmen kann.
Hier ist noch nicht berücksichtigt, dass Elementarsignale auch nach ihrer Aktivität, also Feuerrate eingeteilt werden könnten, z. B. durch Bildung von Feuerraten-Intervallen.
Die Klasseneinteilung von analogen Feuerraten in Feuerratenintervalle ist eine Hauptaufgabe der Digitalisierungsschaltungen des Gehirns, die (nach Ansicht des Autors) vornehmlich durch die Zellsäulen der Cortexrinde realisiert werden. Näheres dazu im zurzeit noch unveröffentlichten Teil 3 und 4 dieser Monografie, deren Herausgabe als eigenständiges Werk geplant ist.
Jedem Elementarsignal entspricht im inversen Cerebellum eine Purkinjegruppe. Ebenso entspricht jedem Komplexsignal im direkten Cerebellum auch eine Purkinjegruppe. Während wir uns also die Purkinjegruppen des inversen Cerebellums auf einer Geraden aufgereiht denken könnten, müssten die Purkinjegruppen des direkten Cerebellums auf Grund ihrer ungeheuren Anzahl auf einer extrem langen Linie aufgereiht werden. Diese wäre auf Grund des Potenzierungstheorems so ungeheuer lang, dass wir sie niemals als gerade Linie in unserem menschlichen Körper unterbringen könnten. Bei Platzmangel hat die Natur jedoch eine gute Lösung parat. Die Gerade wird gebogen und gefaltet. So entstehen die großen Oberflächen im Darm oder in der Lunge. Im Cerebellum ist es analog. Durch die starke Faltung (Wellenberge und Wellentäler) wird eine Linie (bzw. Fläche) mit den Purkinjegruppen soweit zusammengestaucht, dass sie das inverse Cerebellum außen umgibt. Innen liegt - leicht länglich - das inverse Cerebellum (Wurm). Außen liegen die stark gefalteten Flächen des direkten Cerebellums, fast unendlich fein gefaltet und daher entfaltet eine riesige Fläche.
Theorem 2.32: Faltungstheorem des direkten Cerebellums
Die riesige Anzahl von Purkinjegruppen des direkten Cerebellums kann nur dadurch in der Kleinhirnrinde untergebracht werden, weil diese Fläche durch extreme und wiederholte Faltung in dem relativ kleinen verfügbaren Raum untergebracht wird. Das inverse Cerebellum dagegen bildet einen relativ geraden Körper in der Mitte dieses paarigen Organs.
Ebenso hätte der Kleinhirnkern des inversen Cerebellums aus n positiven und n negativen Kernneuronen sein Pendant in einem direkten Cerebellumkern aus 2n positiven und negativen Kernneuronen. Auch die Olive unterliegt einer solchen Zweiteilung in eine direkte Olive mit sehr vielen Neuronen und eine inverse mit deutlich weniger Neuronen.
Erwägt man noch, dass es im Gehirn sowohl aufsteigenden Signale - die afferenten Signale - als auch die absteigenden Signale - die efferenten Signale - gibt, und jede dieser Signalarten ein eigenes direktes und ein eigenes inverses Cerebellum besitzt, so kommt man auf vier Cerebelli und vier Kleinhirnkerne.
Diese Theorie ist nicht so abwegig, wie es scheinen könnte. Neurologen unterscheiden beim Menschen und bei höheren Säugetieren tatsächlich vier Kleinhirnkerne: den Nucleus fastegii, den Nucleus globosus, den Nucleus emboliformis und den Nucleus dentatus.
Theorem 2.33: Theorem der vier Kleinhirnkerne
Da es im Gehirn ein afferentes und ein efferentes System gibt und jedes von ihnen ein direktes und ein inverses Cerebellum nutzt, gibt es auch vier Kleinhirnkerne: den Nucleus fastegii, den Nucleus globosus, den Nucleus emboliformis und den Nucleus dentatus.
Da das Cerebellum ein paarig angelegtes Organ ist, verdoppelt sich die Anzahl seiner Teilelemente, wobei jeweils ein Teilelement für die linke Körperhälfte, das andere für die rechte Körperhälfte zuständig ist, während im Wurm beide Anteile vertreten sind.
Zu beachten ist, dass Cortex- und Cerebellumaxone beim Übergang von Cortex zum Cerebellum und umgekehrt jeweils auf die andere Seite kreuzen.
Da nach Ansicht des Autors das afferente System rekursiv aufgebaus ist, weil der Output der Stufe 1 als Input für eine weitere, afferente Stufe 2 verwendet wird, deren Output die nächsthöhere Stufe speist und sich diese Rekursivität wiederholt, besitzt der Nucleus dentatus als direkter Kleinhirnkern des afferenten Systems eine schier unendliche Anzahl von Kernneuronen, das zugehörige afferente direkte Cerebellum eine ebenso unglaublich große Anzahl von Purkinjegruppen und eine nahezu perfekte Faltung, um die mit Zweierpotenzen wachsende Zahl von Komplexsignalen überhaupt in einer flächenhaften Cerebellumrinde unterzubringen.
ISBN 978-3-00-037458-6ISBN 978-3-00-042153-2
Monografie von Dr. rer. nat. Andreas Heinrich Malczan