Vertebrate brain theory

5.3  Magnitude diagramm, image diagramm, radius vector and phase angle in plane divergence grids

Definition: Great Size Diagram

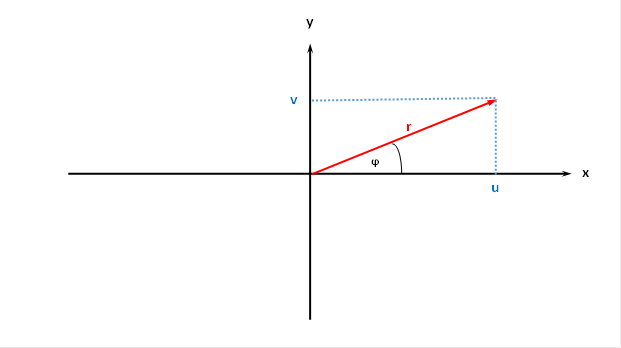Figure 54 - Great Size Diagram in Polar Coordinates

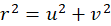             (3.1.1)

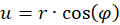           (3.1.2)

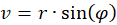            (3.1.3)

This also means that

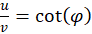                 (3.1.4)

We refer to the quantity φ as the phase angle in the original size diagram.

If u and v are motor variables describing the muscle tension of four muscles of a joint with two degrees of freedom, each periodic movement is represented in the great magnitude diagram by a curve graph representing a Lissajous figure. If, for example, the arm is rotated, a closed circular line is created in the corresponding great magnitude diagram. From the curve graphs it is therefore also possible to infer the type of movement. If you write a figure eight in the air with an outstretched arm, this figure eight - possibly slightly distorted - can be found in the great magnitude diagram. If you write any number or letter in the air with an outstretched arm, exactly this figure appears in the great-size diagram, even if it is shown slightly distorted.

Definition: Image size diagram

The quotient

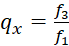
is the quotient of the fire rates f3 and f1 of a plane divergence grating.

The quotient

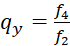
is the quotient of the fire rates f4 and f2 of a plane divergence grating. Let it be

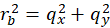             (3.1.5)

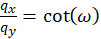               (3.1.6)

We refer to the size ω as phase angle in the image size diagram.

Phase angle theorem

The following applies to the phase angle ω in the image size diagram of a divergence grating

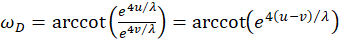                      (3.1.7)