Vertebrate brain theory
ISBN
978-3-00-064888-5
Monograph of Dr. rer. nat. Andreas Heinrich Malczan
5.4. Theory of plane convergence grids
Plane convergence gratingsreverse the signal divergence caused by plane divergence gratings.
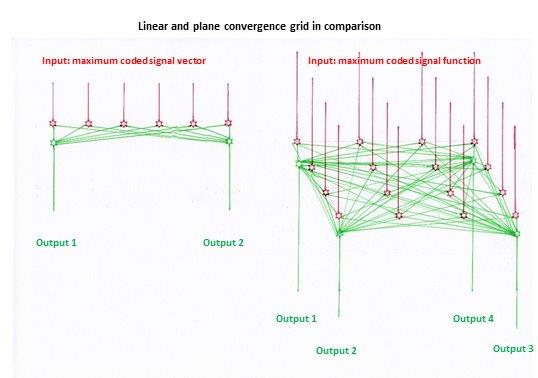
Figure 55 - Linear and plane divergence grating in comparison
We want to determine the output of a plane convergence lattice under the simplifying assumption that due to the lateral inhibition only one output neuron is active and is located exactly at the extreme point of the corresponding divergence lattice. The output of the divergence lattice should be topologically well ordered in the convergence lattice. Of its many input neurons, only the neuron with the coordinates P(xo, yo) is still active in which the excitation function of the divergence lattice has its maximum.
Later, we can consider how the results change when a relatively small population of neurons is active instead of one.
The output of the active neuron propagates along the axons of the interneurons to the corners of the square, where it reaches a total of four output neurons. Again, we assume an exponential damping as in the divergence lattice.
A representation in the coordinate system may facilitate the observation. We choose the same arrangement as in the divergence grid.
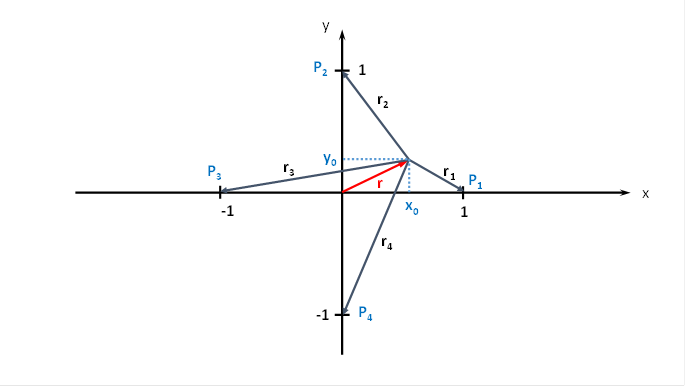
Figure 56 - Plane Convergence Grid in the Cartesian Coordinate System
The following equations are obtained for the radius vectors r1 to r4 using the Pythagorean theorem:
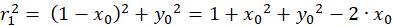 (4.1)
(4.1)
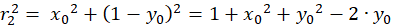 (4.2)
(4.2)
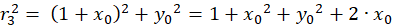 (4.3)
(4.3)
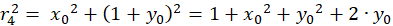 (4.4)
(4.4)
In the plane convergence grid, the excitation spreads from point P(xo, yo) to the neurons at points P1, P2, P3 and P4, which are located at distance 1 from the coordinate origin on the coordinate axes.
Let fmax be the fire rate at point P(x0,y0), which is at the same time the maximum fire rate in the associated divergence grating. During the propagation of this maximum excitation to the output neurons it is exponentially damped. Let f1,k be the rate of fire at point P1, f2,k be that at point P2, f3,k be that at point P3 and f4,k be that at point f4. The Index k indicates that we are looking at the magnitudes of the convergence grid. The neuronal excitation is exponentially damped during propagation to the four output neurons, so that the rates of fire in the output neurons satisfy the following equations
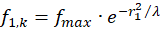 (4.5)
(4.5)
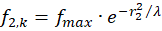 (4.6)
(4.6)
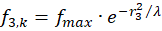 (4.7)
(4.7)
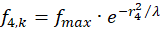 (4.8)
(4.8)
We now calculate the phase angle in the associated image size diagram of the convergence grating.
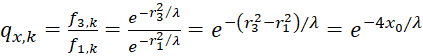 (4.9)
(4.9)
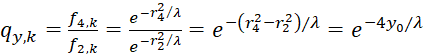 (4.10)
(4.10)
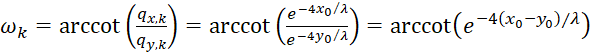 (4.11)
(4.11)
We remember equations (3.1.7) of the divergence lattice
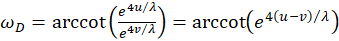 (3.1.7)
(3.1.7)
and recognize that the coordinates of the maximum point in the phase angle of the convergence grid correspond to the original magnitudes u and v of the divergence grid, but that the exponent contains the minus sign, which gives the reciprocal value. A phase shift therefore occurs around π/2.
In the associated divergence grid, according to (3.1.7)
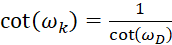
Now we can compare and determine the phase angles in the image size diagram of the divergence grating and the associated convergence grating:
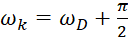 (4.14)
(4.14)
Theorem of phase shift between divergence grating and convergence grating
There is a phase shift between the divergence grid phase and the convergence grid phase from π/2.
Monograph of Dr. rer. nat. Andreas Heinrich Malczan