Gehirntheorie der Wirbeltiere
ISBN
978-3-00-064888-5
Monografie von Dr. rer. nat. Andreas Heinrich Malczan
5.3. Urgrößendiagramm, Bilddiagramm, Radiusvektor und Phasenwinkel in ebenen Divergenzgittern
Definition: Urgrößendiagramm
Die Urgrößen u und v, deren Werte von Rezeptoren gemessen und in Feuerraten transformiert werden, um als Input ein ebenes Divergenzgitter zu speisen, können in einem Koordinatensystem mit Polarkoordinaten dargestellt werden. Während u auf der x-Achse dargestellt wird, ordnen wir v der y-Achse zu.
Diese Darstellung bezeichnen wir hier als Urgrößendiagramm.
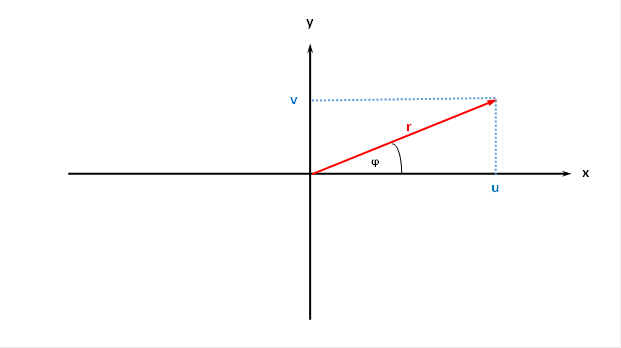
Abbildung 54- Urgrößendiagramm in Polarkoordinaten
Hierbei gelte
![]() (3.1.1)
(3.1.1)
![]() (3.1.2)
(3.1.2)
![]() (3.1.3)
(3.1.3)
Damit gilt auch
![]() (3.1.4)
(3.1.4)
Die Größe φ bezeichnen wir als Phasenwinkel im Urgrößendiagramm.
Sind u und v motorische Größen, die die Muskelspannung von vier Muskeln eines Gelenks mit zwei Freiheitsgraden beschreiben, so wird jede periodische Bewegung im Urgrößendiagramm durch einen Kurvengraphen dargestellt, der eine Lissajous-Figur darstellt. Lässt man beispielsweise den Arm kreisen, so entsteht im zugehörigen Urgrößendiagramm eine in sich geschlossene Kreislinie. Aus den Kurvengraphen kann also auch auf die Art der Bewegung geschlossen werden. Schreibt man mit ausgestrecktem Arm eine Acht in der Luft, so findet sich diese Acht - evtl. leicht verzerrt - im Urgrößendiagramm wieder. Schreibt man irgendeine Ziffer oder einen Buchstaben mit ausgestrecktem Arm in die Luft, so erscheint im Urgrößendiagramm genau diese Figur, auch wenn sie dabei etwas verzerrt dargestellt wird.
Definition: Bildgrößendiagramm
Der Quotient
![]()
sei der Quotient aus der Feuerraten f3 und f1 eines ebenen Divergenzgitters.
Der Quotient
![]()
sei der Quotient aus der Feuerraten f4 und f2 eines ebenen Divergenzgitters. Es sei
![]() (3.1.5)
(3.1.5)
![]() (3.1.6)
(3.1.6)
Die Größe ω bezeichnen wir als Phasenwinkel im Bildgrößendiagramm.
Phasenwinkeltheorem
Für den Phasenwinkel ω im Bildgrößendiagramm eines Divergenzgitters gilt
![]() (3.1.7)
(3.1.7)
Monografie von Dr. rer. nat. Andreas Heinrich Malczan